2変数関数の極値の求め方・計算問題・偏微分について

1. 2変数関数の極値を求める手順
2変数関数 \( f(x, y) \) の極値を求める方法は、次の手順に従います。
1.1. 関数の偏微分を求める
まず、関数 \( f(x, y) \) の各変数について偏微分を求めます。つまり、次のように \( x \) と \( y \) に関して微分を行います。 \[ f_x = \frac{\partial f}{\partial x}, \quad f_y = \frac{\partial f}{\partial y} \]
1.2. 偏微分がゼロとなる点を探す
次に、偏微分がゼロとなる点、つまり、候補となる極値の点を探します。そのために、以下の方程式を解きます。
\[ f_x = 0, \quad f_y = 0 \]
これにより、臨界点 \( (x_0, y_0) \) が得られます。
1.3. 極値の判定
$f_{xx}=A$, $f_{xy}=B$, $f_{yy}=C$とし、$D=B^2-AC$を用いて極値を判定します。
- \(D < 0\) かつ \(A > 0\) のとき、極小点。
- \(D < 0\) かつ \(A < 0\) のとき、極大点。
- \(D > 0\) のとき、極値なし。
これにより、2変数関数の極値を求めることができます。
判別式のイメージは次の通りです。
まず、$A$を二次関数の$x^2$の係数として考えます。
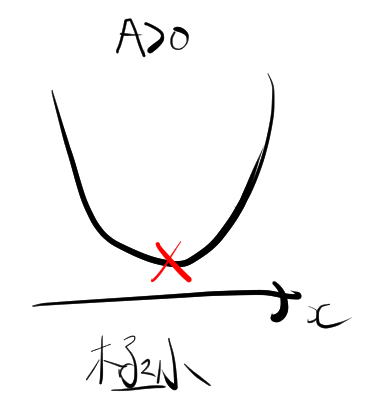
\(A > 0\) かつ \(D < 0\) のとき、実数解を持たないため、グラフは以下のような形になります。
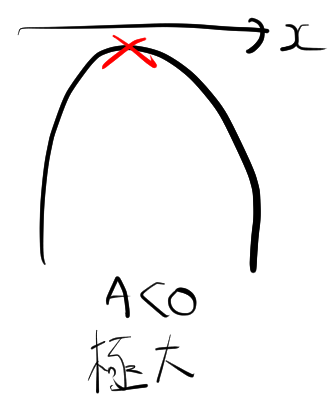
一方、\(A < 0\) かつ \(D < 0\) のとき、同様に実数解を持たないため、グラフは次のような形になります。
2. 極値を求める例題
2.1. 例題1
$$f(x,y)=x^2+xy+y^2$$
2変数関数 \( f(x,y) = x^2 + xy + y^2 \) の極値を求めるために、まず偏微分します。
関数 \( f(x, y) \) の \( x \) に関する偏微分は次のようになります。
\[ \frac{\partial f}{\partial x} = 2x + y \]
同様に、\( y \) に関する偏微分は次のようになります。
\[ \frac{\partial f}{\partial y} = x + 2y \]
極値を求めるために、まず$f_x=f_y=0$となる点を求めます。
\[ \frac{\partial f}{\partial x} = 0 \quad \text{と} \quad \frac{\partial f}{\partial y} = 0 \]
つまり、
\[ 2x + y = 0 \quad \text{(1)} \] \[ x + 2y = 0 \quad \text{(2)} \]
まず、式 (1) より \( y = -2x \) です。これを式 (2) に代入します。
\[ x + 2(-2x) = 0 \]
$$x – 4x = 0 $$
$$x = 0$$
\( x = 0 \) を式 (1) に代入すると、
$$ 2(0) + y = 0 $$
$$y = 0 $$
したがって、 \( (0, 0) \)のとき$f_x=f_y=0$ です。
次に、$f_{xx},f_{xy},f_{yy}$を計算します。
$$A=f_{xx}=2$$
$$B=f_{xy}=1$$
$$C=f_{yy}=2$$
$D=B^2-AC$と置くと、$D=1-4=-3<0$となる。
$(0,0)$のとき、$A>0$かつ$D<0$より、関数$f(0,0)=0$は極小値である。
2.2. 例題2
$$f(x,y)=xy+2x+2y$$
まず、関数 \( f(x, y) = e^x(x^2 + y^2) \) について、偏微分を求めます。
関数 \( f(x, y) \) を \( x \) と \( y \) でそれぞれ偏微分します。
\[ f_x = e^x(x^2 + y^2) + e^x \cdot 2x = e^x(x^2 + y^2 + 2x) \]
\[ f_y = e^x \cdot 2y \]
偏微分がゼロとなる点を探します。
\[ e^x(x^2 + y^2 + 2x) = 0 \]
\( e^x \neq 0 \) なので、 \[ x^2 + y^2 + 2x = 0 \]
\[ e^x \cdot 2y = 0 \]
\( e^x \neq 0 \) なので、
\[ y = 0 \]
これを \( f_x = 0 \) の方程式に代入します。
$$x^2 + 0^2 + 2x = 0 $$
$$ x(x + 2) = 0 $$
\( x = 0 \) または \( x = -2 \) となります。
したがって、極値の候補の点は \( (0, 0) \) と \( (-2, 0) \) です。
次に、$f_{xx},f_{xy},f_{yy}$を計算します。
\[ f_{xx} = \frac{\partial}{\partial x} \left( e^x(x^2 + y^2 + 2x) \right) = e^x(x^2 + y^2 + 4x + 2) \]
\[ f_{xy} = \frac{\partial}{\partial y} \left( e^x(x^2 + y^2 + 2x) \right) = e^x \cdot 2y \]
\[ f_{yy} = \frac{\partial}{\partial y} \left( e^x \cdot 2y \right) = e^x \cdot 2 \]
$A=f_{xx},B=f_{xy},C=f_{yy}$とする。
\( (0, 0) \) の場合:
$(0,0)$をA,B,Cを代入すると、$A=2,B=0,C=2$であるため、$D=0-4=-4<0$である。
A>0かつD<0より、\( (0, 0) \) は極小値を持ちます。
\( (-2, 0) \) の場合:
$(-2,0)$をA,B,Cを代入すると、
$$A=e^{-2}(4-8+2)=-2e^{-2}$$
$$B=e^{-2}\cdot 0=0$$
$$C=2e^{-2}$$
\[ D = 0-(-2e^{-2})\cdot 2e^{-2} = 4e^{-2} > 0 \]
$D>0$より、\( (-2, 0) \) は極値を持ちません。
したがって、
\( (0, 0) \) は極小値を持ちます。
\( (-2, 0) \) は極値を持ちません。