
はるか
複素数の計算って、なんかベクトルと似ている気がする。

ふゅか
そうね、複素数をベクトルのように考えて図形的に考えることもできるからね!
1. 複素数のベクトル的な考え方
複素数を
α,zとする。このとき、
z−αは複素数平面上では
αから
zを表しています。

はるか
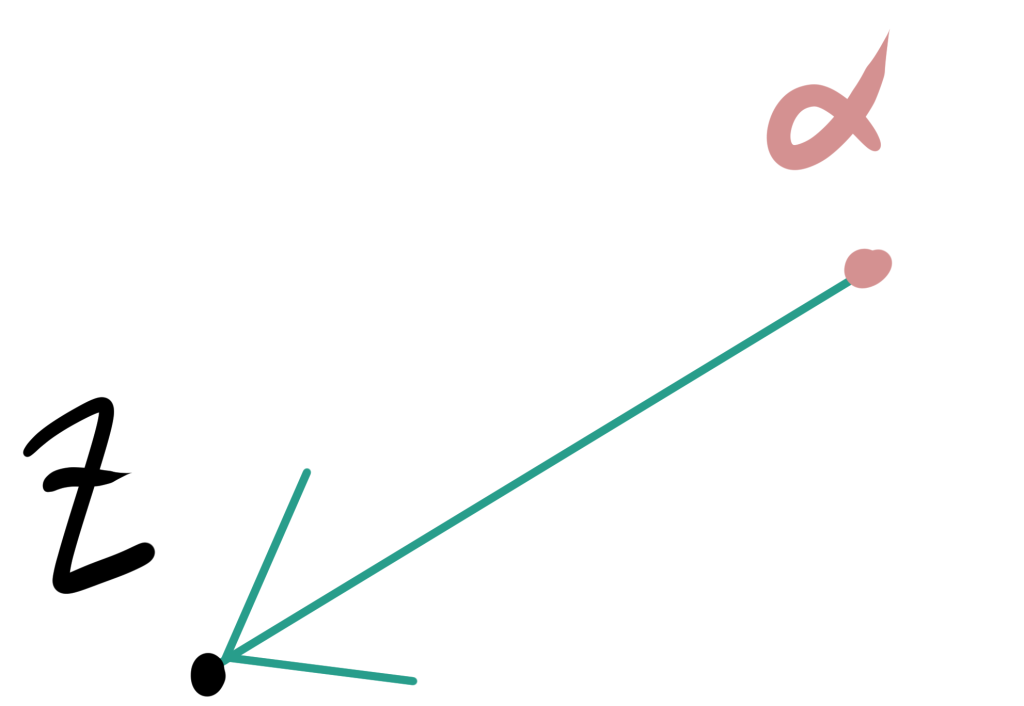
そのため、∣z−α∣はαからzまでの距離を表します。
例えば、
∣z−α∣=r
はαからzまでの距離がr(一定)になっているということを表します。
1.1. 図形的に考える例題
zを複素数としたときに、
zを複素数平面上で図示せよ。
iは虚数単位とする。
(1)∣z+1∣=∣z−i∣
(2)∣z+3i∣=3
から
zまでの距離とiからzまでの距離が等しいという図形である。
距離が等しいというイメージは以下のようになります。
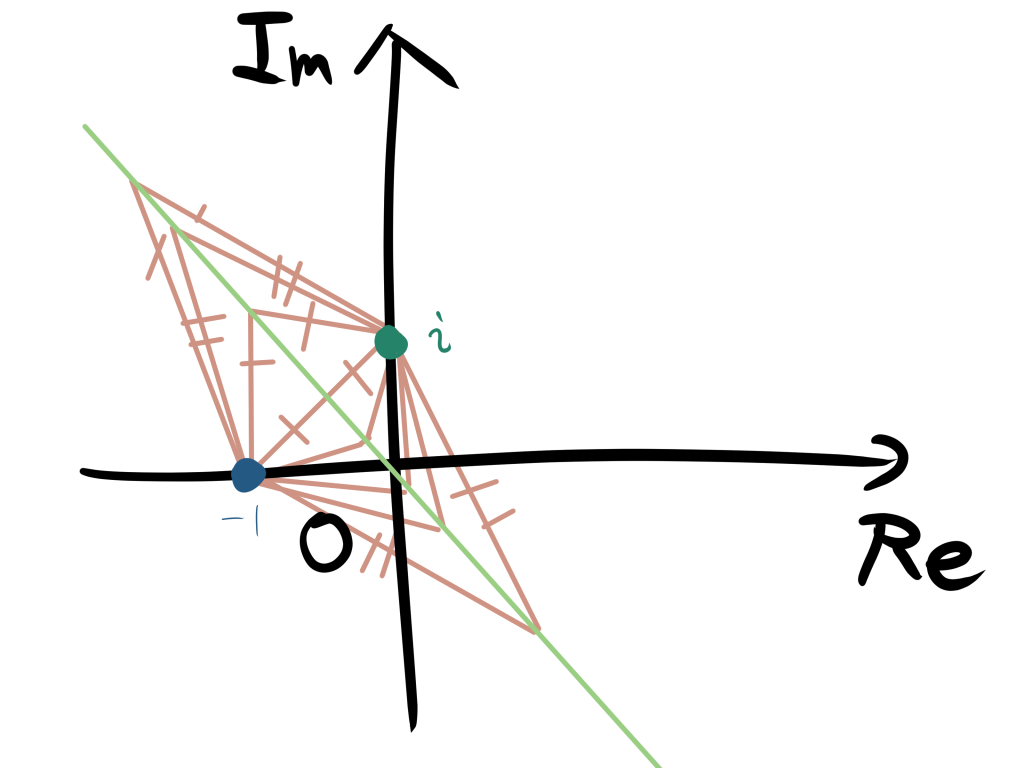
そのため、直線であることがわかるから以下のようになります。
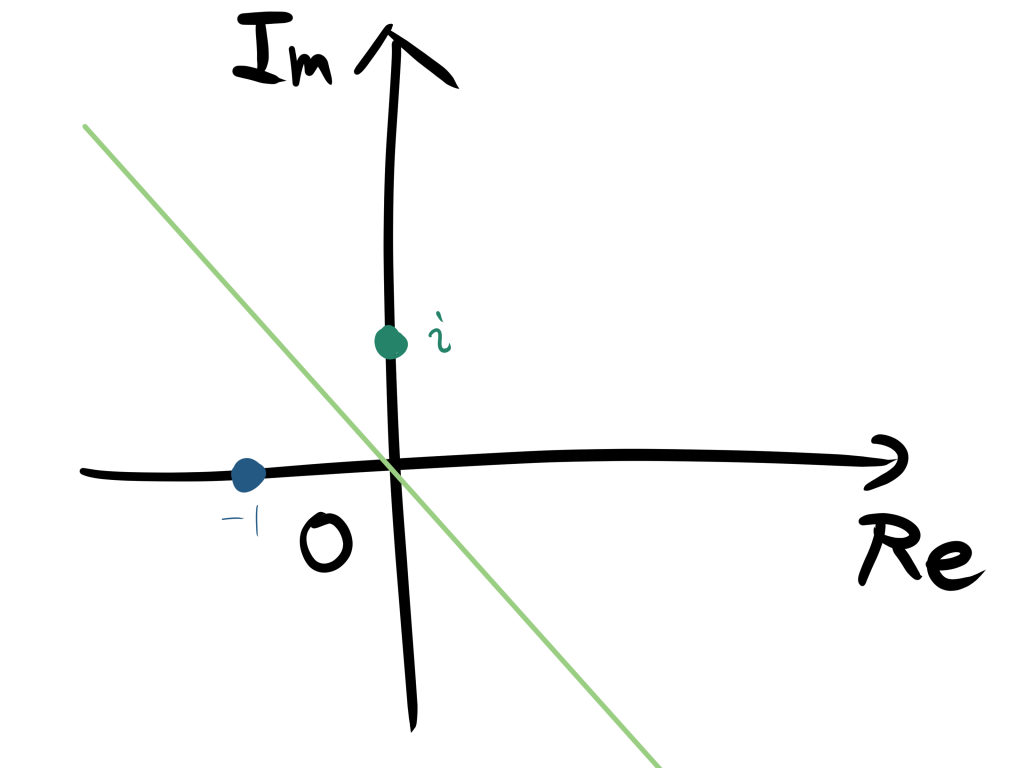

はるか
−1から
zまでの距離と
iから
zまでの距離が等しいから、直線になる。
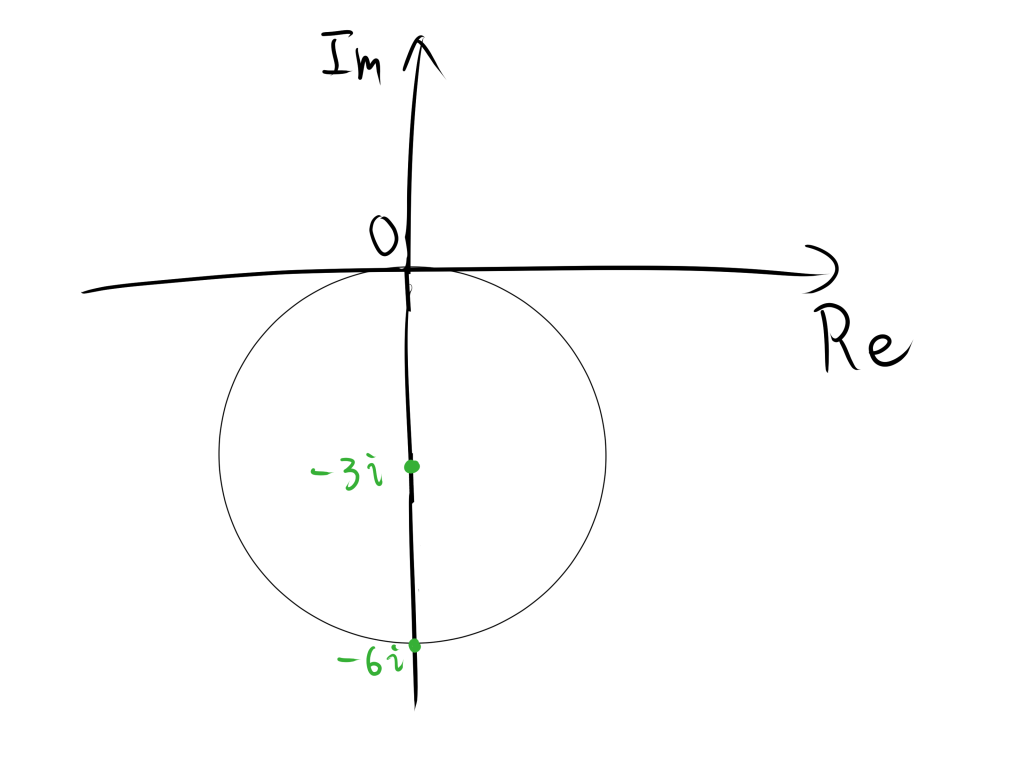
(2) −3iからzまでの距離が3である図形である。
イメージは以下のようになります。
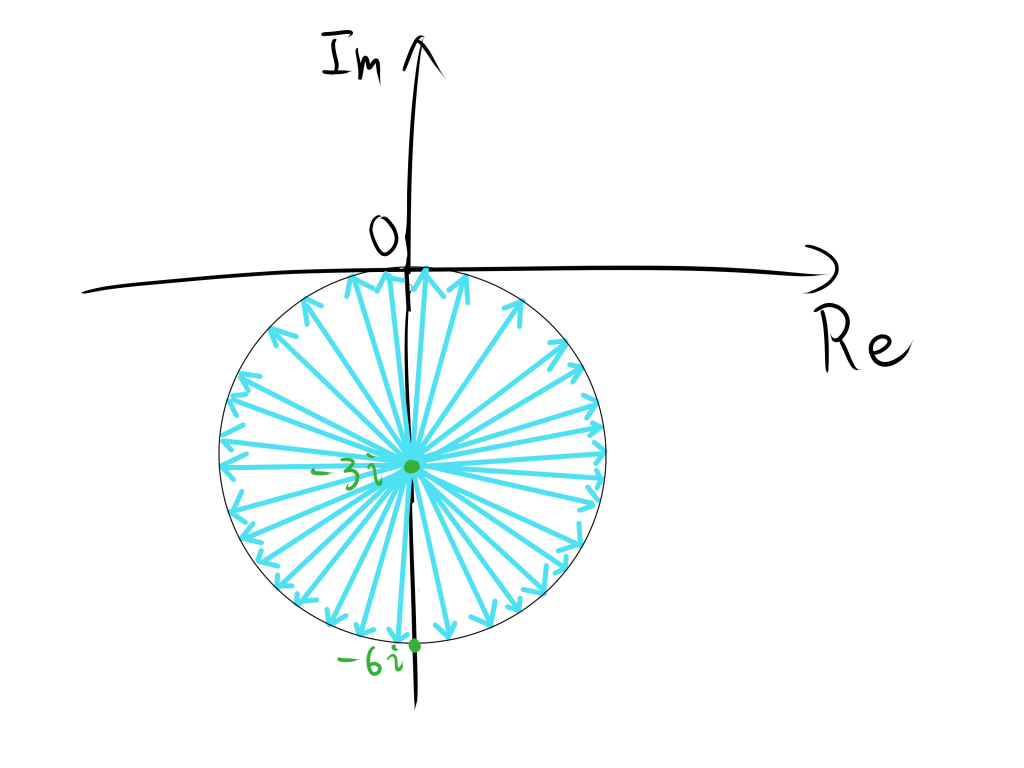
そのため、−3iを中心とする半径3の円であることがわかるから以下のようになります。
2. ベクトル的な考えができる理由
この疑問は計算的に考えると解決することができます。
ベクトルについてまず考えます。
OA=[a1a2]OB=[b1b2]とする。
AB=OB−OA
=[b1−a1b2−a2]
単位ベクトルe1=[10]、e2=[01]を用いて表すと、
AB=[b1−a1b2−a2]
=(b1−a1)e1+(b2−a2)e2
次に複素数について考えます。虚数単位をiとします。
複素数a,bを以下のようにあらわすとする。
a=a1+a2i
b=b1+b2i
このとき、a1,a2,b1,b2は実数である。
b−a=(b1−a1)+(b2−a2)i
ベクトルで似たような形の数式が出てきましたよね。では、ベクトルは成分表示されているので、複素数の成分表示を考えてみましょう。
ここで、単位ベクトルer=[10]、ei=[0i]を用いて表すと、b−aの成分は以下のようにあらわすことができます。
(b1−a1)er+(b2−a2)ei
=[b1−a1b2−a2]
b1−a1は実軸の成分、b2−a2は虚軸の成分と考えることができる。
また、複素数平面は虚軸と実軸で構成されています。虚軸は純虚数のみで構成されているためeiを実数倍すると、虚軸を表すことができます。実軸も同様にすることができます。
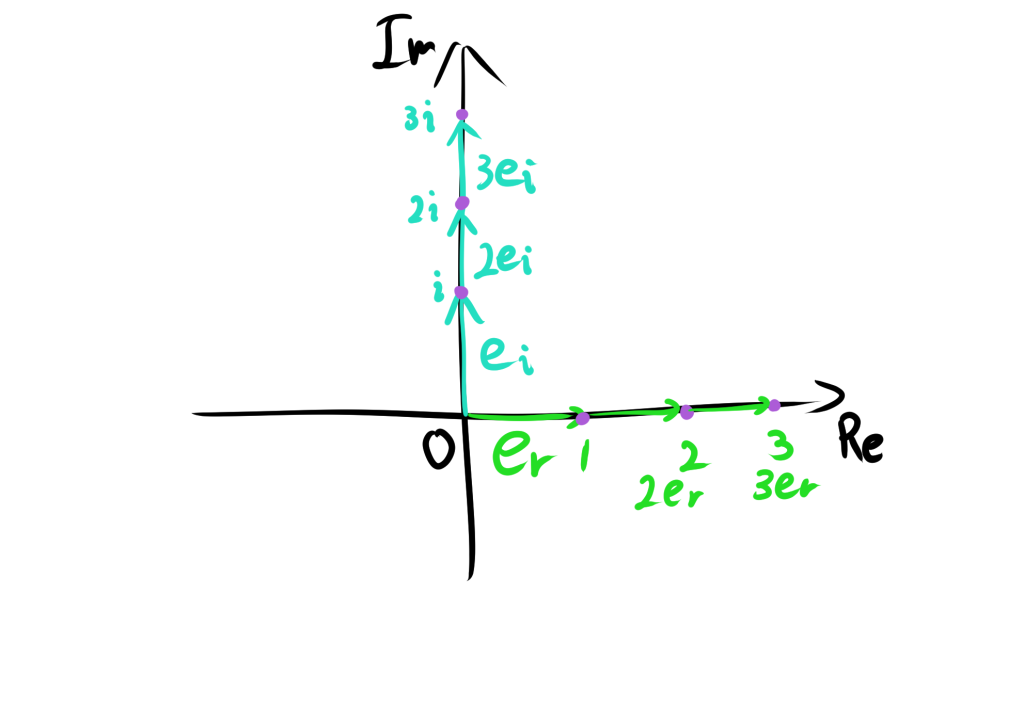
eiとerの内積は0になるため、垂直に交わっているので、eiとerは複素数平面を表すことができます。
ei⋅er=0
だから、複素数平面でもベクトルのような考えをすることができます。











