ベクトルとは？意味と高校数学と大学数学の違い

1. ベクトルとは

ベクトルとは、「大きさ」と「向き」を持つ量のことです。例えば、風の強さとその吹く方向、力の強さとその向きなどがベクトルで表されます。

数学的には、ベクトルは矢印で表され、向きが示す方向と矢印の長さが示す大きさを持ちます。例えば、平面上のベクトル \(\vec{a}\) は \((x, y)\) という形で表され、\(x\) と \(y\) はそれぞれの軸に対する成分です。

1.1. 始点と終点

ベクトルが始まる点のことを始点といい、矢印が終わる点を終点という。

1.2. 等しいベクトル

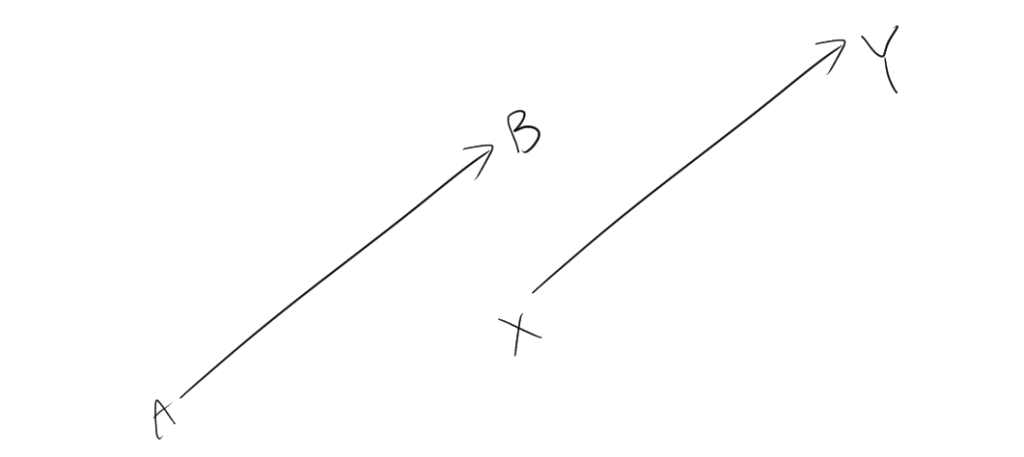
向きと大きさが等しいベクトルは同じベクトルになる。つまり、位置は関係ないのです。例えば、$\overrightarrow{AB}$と$\overrightarrow{XY}$の向きと大きさが等しいとき、

$$\overrightarrow{AB}=\overrightarrow{XY}$$

となる。

1.3. ベクトルの例

ベクトル \(\vec{a} = (3, 4)\) は、x方向に3、y方向に4だけ進むような向きを持っています。このベクトルの大きさは、\(\sqrt{3^2 + 4^2} = 5\) となります。

2. 高校数学と大学数学の違い

高校数学と大学数学における「ベクトル」という言葉の意味には、取り扱う視点と概念の広がりに違いがあります。

2.1. 高校数学におけるベクトル

高校数学では、ベクトルは「大きさ」と「向き」を持つ矢印として捉えられています。平面ベクトル（2次元）や空間ベクトル（3次元）を使い、ベクトルの成分表示や演算（加法、スカラー倍、内積）を扱います。視覚的に理解しやすい「矢印」としてのベクトルのイメージが強調されます。

2.2. 大学数学におけるベクトル

大学数学（線形代数）におけるベクトルは、より抽象的な概念に拡張されます。ベクトル空間を導入し、次元が高次元（n次元）や無限次元のベクトルも扱います。大学では、ベクトルを単なる「矢印」としてではなく、「ベクトル空間の元」として考え、より一般的な構造や性質に注目します。ようは、集合の一要素として考えます。ベクトル空間の元として次のようなものがあります。

3. 高校数学と大学数学の違い

3.1. 次元の扱い

高校では2次元や3次元ベクトルが中心ですが、大学では高次元（場合によっては無限次元）のベクトルを扱います。

3.2. 視覚的 vs 抽象的

高校では矢印としての視覚的理解が重視されますが、大学ではより抽象的な「空間の要素」としての理解が求められます。