【図解】ベクトルの加法と減法の意味と分解について

はるか

ベクトルの加法と減法か…基本だけど、大事。

ふゅか

うん、どっちも直感的に理解できるといいよね！図を見ながら覚えると分かりやすいと思う！

1. ベクトルの加法

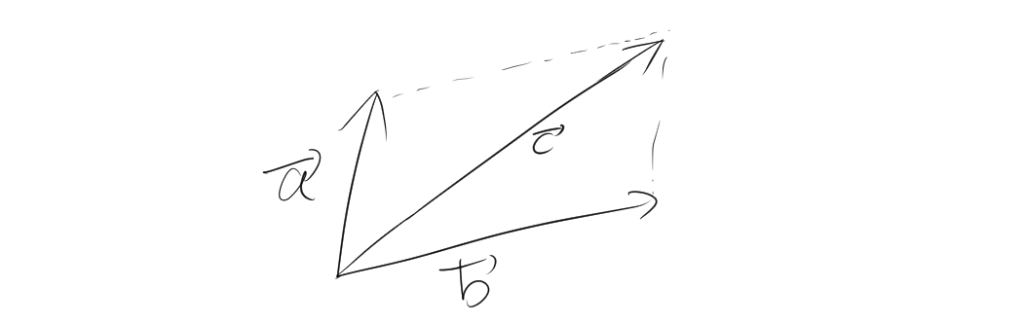
2つのベクトル \(\vec{a}\) と \(\vec{b}\) の和 \(\vec{c} = \vec{a} + \vec{b}\) は、ベクトルの始点と終点をつなぐことで求められます。ベクトル \(\vec{a}\) の終点からベクトル \(\vec{b}\) を伸ばすと、 \(\vec{c}\) になります。また、ベクトル \(\vec{b}\) の終点からベクトル \(\vec{a}\) を伸ばすと、同様に\(\vec{c}\) になります。

ふゅか

ベクトルの加法って、2つのベクトルをくっつけて、終点をつなぐことで求めるんだよね！

はるか

そう。終点から次のベクトルを足すだけ。

1.1. ベクトルの加法の分解

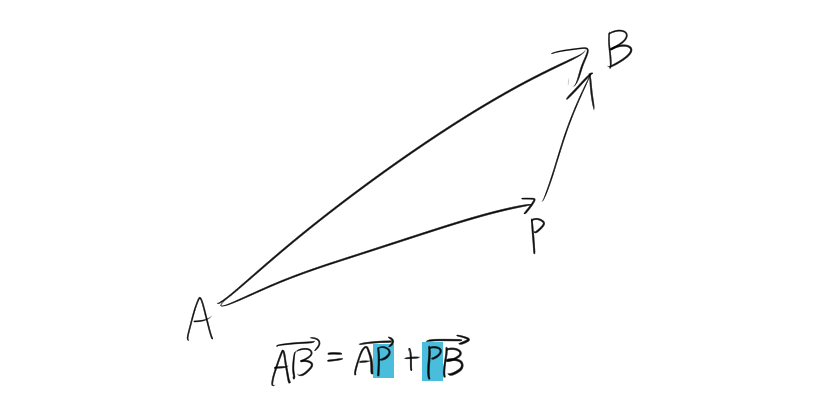
ベクトル \(\overrightarrow{AB}\) は次のように表すことができます。
\[ \overrightarrow{AB} = \overrightarrow{AP} + \overrightarrow{PB} \]

この図からもわかるように、ベクトルの加法ではベクトル同士を並べてつなぎ、その結果のベクトルを求めるのが基本的な考え方です。

2. ベクトルの減法

次に、2つのベクトル \(\vec{a}\) と \(\vec{b}\) の差 について考えます。ベクトルの差 \(\vec{c} = \vec{a} – \vec{b}\) は、ベクトル \(\vec{b}\) の 逆向きのベクトル（\(-\vec{b}\)）を使って計算します。ベクトル \(\vec{a}\) の始点から \(-\vec{b}\) を加えることで、差のベクトル \(\vec{c}\) を求めることができます。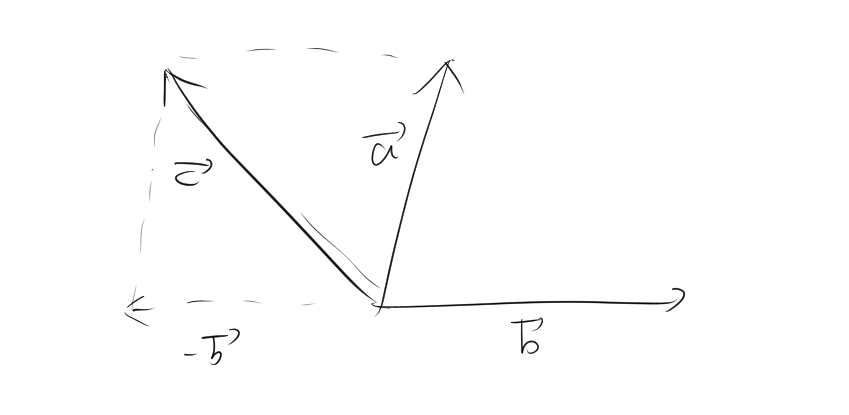

2.1. ベクトルの減法の分解

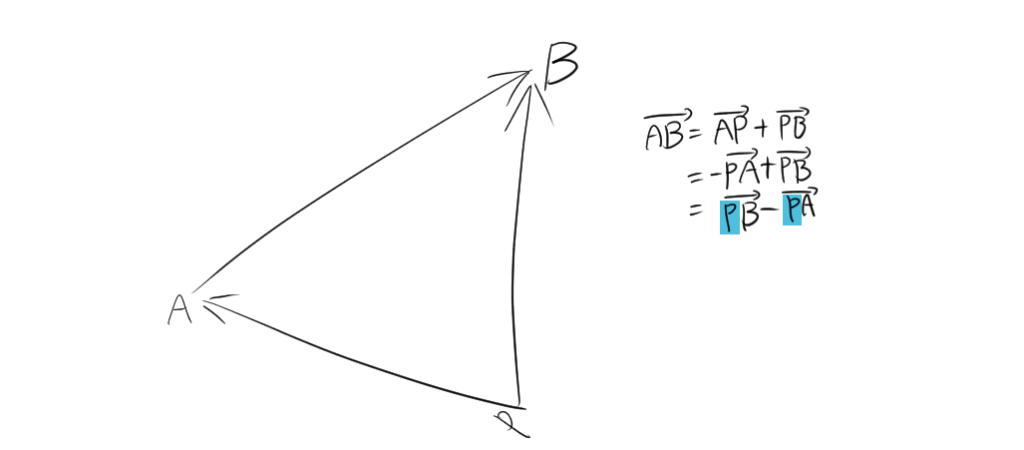
ベクトル \(\overrightarrow{AB}\) はベクトルの加法の性質より、

\[ \begin{aligned} \overrightarrow{AB} &= \overrightarrow{AP} + \overrightarrow{PB} \\ &= -\overrightarrow{PA} + \overrightarrow{PB} \\ &= \overrightarrow{PB} – \overrightarrow{PA} \end{aligned} \]

このベクトルの式を図にすると、

はるか

図で見るとわかりやすい。向きが反対になるのがポイント。