ベクトルの微分の意味と公式について

1. ベクトルの微分
ベクトルの微分は、力学や電磁気学、最適化、機械学習など多くの分野で重要な役割を果たします。以下の3つのケースに焦点を当ててベクトルの微分を解説します。この3つに分けて、今何の計算をしているのか理解しましょう。
2. ベクトルをスカラーで微分する
2.1. スカラーで微分すると起こること
$$ \dfrac{d}{dt} \mathbf{a}= \left(\dfrac{da_1}{dt} , \dfrac{da_2}{dt} , \cdots ,\dfrac{da_n}{dt} \right) $$
一方で、$\mathbf{a}(t) = \begin{pmatrix} a_1(t) \\ a_2(t) \\ \vdots \\ a_n(t) \end{pmatrix}$ であれば、
$$ \dfrac{d}{dt} \mathbf{a}= \begin{pmatrix} \dfrac{da_1}{dt} \\ \dfrac{da_2}{dt} \\ \vdots \\\dfrac{da_n}{dt} \end{pmatrix} $$
2.2. 具体例
$\mathbf{a}(t) = \begin{pmatrix} t^2 \\ \sin(t) \\ e^{2t} \end{pmatrix}$ の場合、
$$ \dfrac{d\mathbf{a}}{dt} = \begin{pmatrix} 2t \\ \cos(t) \\ 2e^{2t} \end{pmatrix} $$
2.3. ベクトルをスカラーで微分したときの公式
$$\begin{align*} \dfrac{d}{dt} (\mathbf{a} + \mathbf{b}) &= \dfrac{d}{dt} \mathbf{a} + \dfrac{d}{dt} \mathbf{b} \\ \dfrac{d}{dt} (f\mathbf{a}) &= \dfrac{df}{dt} \mathbf{a} + f \dfrac{d}{dt} \mathbf{a} \\ \dfrac{d}{dt} (\mathbf{a} \cdot \mathbf{b}) &= \dfrac{d}{dt} \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \dfrac{d}{dt} \mathbf{b} \\ \dfrac{d}{dt} (\mathbf{a} \times \mathbf{b}) &= \dfrac{d}{dt} \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \dfrac{d}{dt} \mathbf{b} \end{align*}$$
外積はベクトルの次元が3になります。
3. スカラーをベクトルで微分する
スカラー関数 $f(x_1,x_2,\cdots,x_n)$ をベクトル $\mathbf{x}$ で微分すると、勾配ベクトル が得られます。これは、各変数に関する偏微分を集めたベクトルです。
$$ \dfrac{\partial f}{\partial \mathbf{x}} = \left( \dfrac{\partial f}{\partial x_1} , \dfrac{\partial f}{\partial x_2} , \cdots \dfrac{\partial f}{\partial x_n} \right) $$
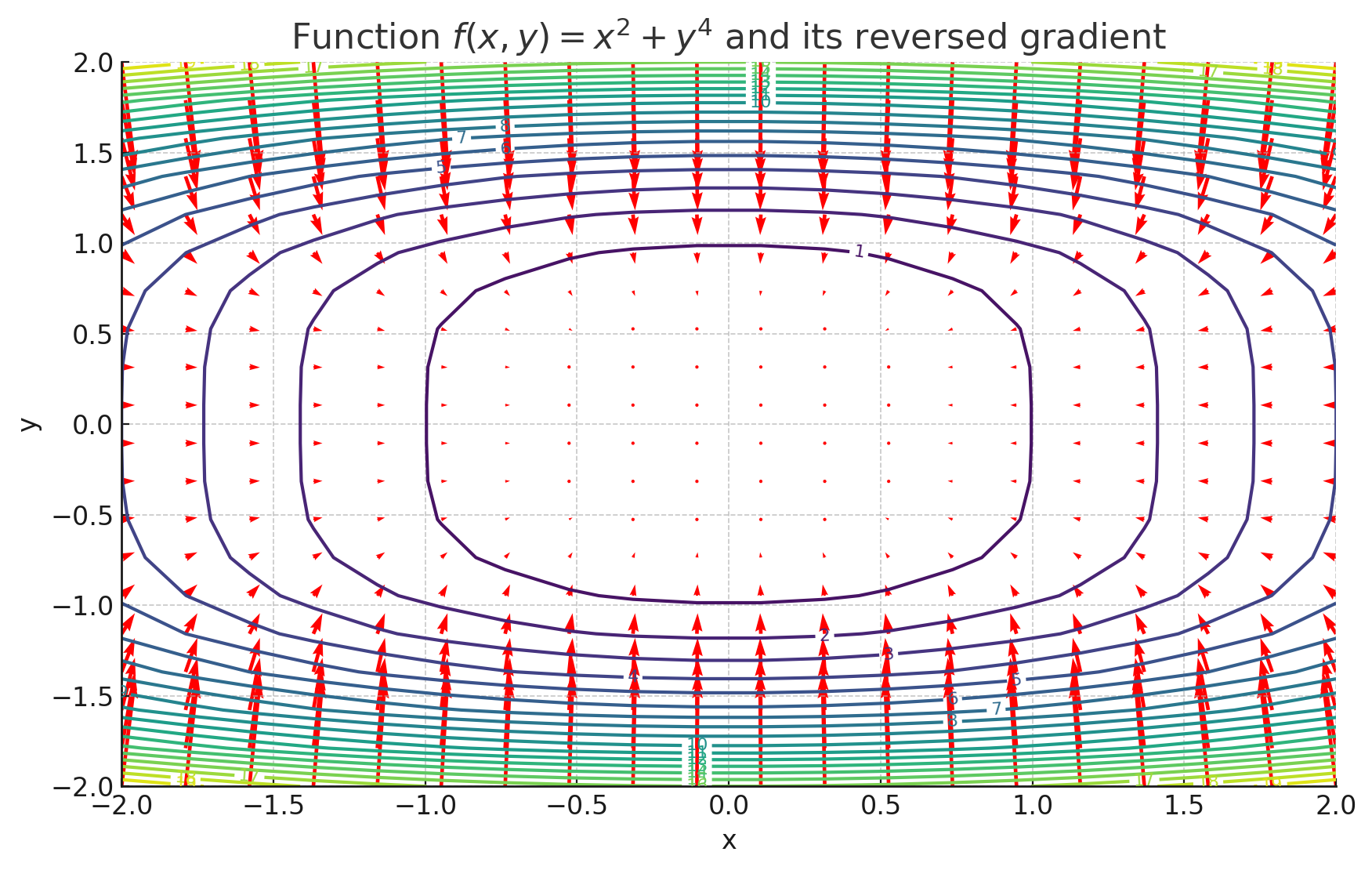
3.1. 具体例
$f(x_1,x_2,x_3) = x_1^2 + x_2^2 + x_3^2$ の場合、$\mathbf{x}=(x_1,x_2,\cdots,x_3)$で微分すると、
$$ \dfrac{\partial f}{\partial \mathbf{x}} = ( 2x_1 , 2x_2 , 2x_3 ) $$
3.2. スカラーをベクトルで微分したときの公式
\[\begin{align*} \frac{\partial}{\partial \mathbf{x}} (\mathbf{a} \cdot \mathbf{x}) =\frac{\partial}{\partial \mathbf{x}}(\mathbf{x} \cdot \mathbf{a})&= \mathbf{a} \\ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x} \cdot \mathbf{x}) &= 2\mathbf{x}\\ \frac{\partial}{\partial \mathbf{x}} \left( (\mathbf{x} – \mathbf{a})^T (\mathbf{x} – \mathbf{a}) \right) &= 2(\mathbf{x} – \mathbf{a}) \\ \frac{\partial}{\partial \mathbf{x}} (\mathbf{x}^T A \mathbf{x}) &= (A + A^T) \mathbf{x} \end{align*}\]
4. ベクトルをベクトルで微分する
ベクトル関数 $\mathbf{a}(\mathbf{x})$ をベクトル変数 $\mathbf{x}$ で微分すると、行列が得られます。
$$ \dfrac{\partial }{\partial \mathbf{x}} \mathbf{a}= \begin{pmatrix} \dfrac{\partial a_1}{\partial x_1} & \dfrac{\partial a_2}{\partial x_1} & \dots & \dfrac{\partial a_n}{\partial x_1} \\ \dfrac{\partial a_1}{\partial x_2} & \dfrac{\partial a_2}{\partial x_2} & \dots & \dfrac{\partial a_n}{\partial x_2} \\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{\partial a_1}{\partial x_n} & \dfrac{\partial a_2}{\partial x_n} & \dots & \dfrac{\partial a_n}{\partial x_n} \end{pmatrix} $$
4.1. 具体例
$\mathbf{a}= ( x_1 x_2 , x_2 x_3 , x_3 x_1 )$ を$\mathbf{x}=(x_1,x_2,\cdots,x_3)$で微分すると、
\[ \begin{align*} \dfrac{\partial }{\partial \mathbf{x}} \mathbf{a} &= \begin{pmatrix} \dfrac{\partial a_1}{\partial x_1} & \dfrac{\partial a_2}{\partial x_1} & \dfrac{\partial a_3}{\partial x_1} \\ \dfrac{\partial a_1}{\partial x_2} & \dfrac{\partial a_2}{\partial x_2} & \dfrac{\partial a_3}{\partial x_2} \\ \dfrac{\partial a_1}{\partial x_3} & \dfrac{\partial a_2}{\partial x_3} & \dfrac{\partial a_3}{\partial x_3} \end{pmatrix} \\ &= \begin{pmatrix} x_2 & 0 & x_3 \\ x_1 & x_3 & 0 \\ 0 & x_2 & x_1 \end{pmatrix} \end{align*} \]
4.2. ベクトルをベクトルで微分したときの公式
$$\begin{align*} \frac{\partial x}{\partial x} &= I_n \\ \frac{\partial}{\partial x}(Ax) &= A^T \\ \end{align*}$$
ベクトルを入力とし、ベクトルを返す関数 \( f : \mathbb{R}^n \to \mathbb{R}^n \) および \( g : \mathbb{R}^n \to \mathbb{R}^n \) を合成したとき、合成関数の微分に関して次の関係が成り立ちます。
\[ \dfrac{\partial}{\partial \mathbf{x}} g(f(\mathbf{x})) = \dfrac{\partial f}{\partial \mathbf{x}} \cdot \dfrac{\partial g}{\partial \mathbf{y}} \]




