【ベクトル解析】ベクトルの発散(ダイバージェンス)の定義・意味・例題について

1. 発散(ダイバージェンス)とは
ベクトルのダイバージェンス(divergence、発散)は、ベクトル場の各点での「湧き出し」を表すスカラー量です。
\[ \text{div} \mathbf{F} = \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} \]
ここで、\(\nabla \cdot \mathbf{F}\) は「ナブラ(∇)とベクトル場(\(\mathbf{F}\))の内積」を意味し、それぞれの成分の偏微分の和を取ることで計算されます。
1.1. ダイバージェンスの計算例
簡単なベクトル場 \(\mathbf{F} = (x, y, z)\) に対するダイバージェンスを計算してみましょう。
\[ \text{div} \mathbf{F} = \frac{\partial x}{\partial x} + \frac{\partial y}{\partial y} + \frac{\partial z}{\partial z} = 1 + 1 + 1 = 3 \]
この場合、各成分の偏微分はそれぞれ 1 となり、全ての成分の和としてダイバージェンスは 3 となります。
2. 発散(ダイバージェンス)の意味
2.1. 立方体に水が流れる状況を想像する
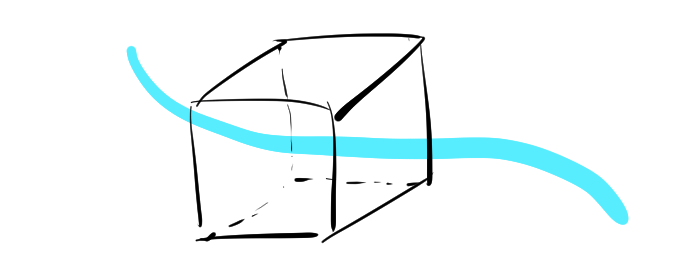
考えやすい例として、川のように水が流れている空間をイメージしましょう。その中に立方体を入れた場合、さまざまな方向から水が流れ込み、また外へ流れ出す様子が観察できます。
立方体に対して「どれだけ水が外へ流れ出しているか」(流出量)と「どれだけ水が立方体に流れ込んでいるか」(流入量)を考えます。
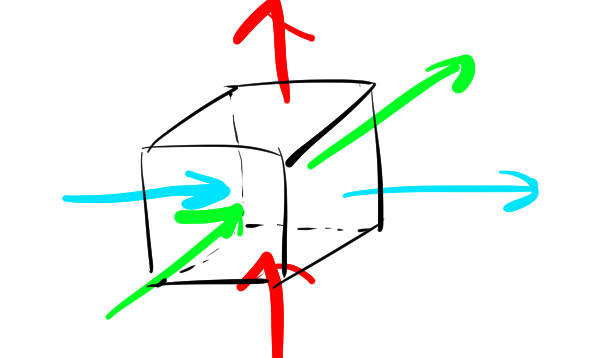
立方体における水の流入量と流出量を以下のように考えてみましょう。
- \(x\)方向:
- 流入量 = 4
- 流出量 = 5
- \(y\)方向:
- 流入量 = 2
- 流出量 = 3
- \(z\)方向:
- 流入量 = 1
- 流出量 = 2
各方向ごとの流入量と流出量がわかっているので、それを使って立方体全体の正味の流出量を計算します。
- 流入量の合計: \(4 + 2 + 1 = 7\)
- 流出量の合計: \(5 + 3 + 2 = 10\)
正味の流出量は、流出量から流入量を引いた値になります:
\[ \text{正味の流出量} = 10 – 7 = 3 \]
この値は、立方体全体からの正味の流出量を示しています。
2.2. 微小体積における発散の導出
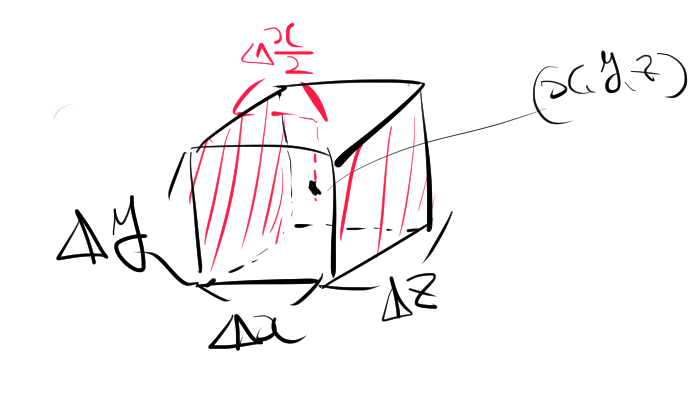
微小直方体を \(x, y, z\) 軸に平行な面で囲まれた体積 \( \Delta x \times \Delta y \times \Delta z \) として、それぞれの方向から流入・流出する水の量を計算します。\(x\)方向の流入と流出の差は次のように表されます。
\[ \text{流出量} – \text{流入量} = V_x \left( x + \frac{\Delta x}{2}, y, z \right) \Delta y \Delta z – V_x \left( x – \frac{\Delta x}{2}, y, z \right) \Delta y \Delta z \]
この式をテイラー展開して、\(\Delta x\)が非常に小さい場合を考えます。
\[ V_x \left( x + \frac{\Delta x}{2}, y, z \right) \approx V_x(x, y, z) + \frac{\partial V_x}{\partial x} \cdot \frac{\Delta x}{2} \] \[ V_x \left( x – \frac{\Delta x}{2}, y, z \right) \approx V_x(x, y, z) – \frac{\partial V_x}{\partial x} \cdot \frac{\Delta x}{2} \]
よって、\(x\)方向の流出量と流入量の差は次のようになります。
\[ \left( V_x(x, y, z) + \frac{\partial V_x}{\partial x} \cdot \frac{\Delta x}{2} \right) \Delta y \Delta z – \left( V_x(x, y, z) – \frac{\partial V_x}{\partial x} \cdot \frac{\Delta x}{2} \right) \Delta y \Delta z \] \[ = \left( \frac{\partial V_x}{\partial x} \cdot \Delta x \right) \Delta y \Delta z \]
同様にして、\(y\)方向と\(z\)方向についても計算すると、
\[ \text{y方向の正味の流出量} = \frac{\partial V_y}{\partial y} \cdot \Delta x \Delta y \Delta z \] \[ \text{z方向の正味の流出量} = \frac{\partial V_z}{\partial z} \cdot \Delta x \Delta y \Delta z \]
これらをすべて合計すると、全体の正味の流出量は次のようになります。
\[ \text{正味の流出量} = \left( \frac{\partial V_x}{\partial x} + \frac{\partial V_y}{\partial y} + \frac{\partial V_z}{\partial z} \right) \Delta x \Delta y \Delta z \]
最終的に、体積 \( \Delta x \Delta y \Delta z \) で割ると、単位体積あたりの正味の流出量、すなわち発散 \( \text{div} \) が得られます。
\[ \text{div} \mathbf{V} = \frac{\partial V_x}{\partial x} + \frac{\partial V_y}{\partial y} + \frac{\partial V_z}{\partial z} \]
3. 問題
3.1. 問題 1
ベクトル場 \( \mathbf{F}(x, y, z) = (F_1, F_2, F_3) \) のダイバージェンスは次の式で与えられます:
\[ \nabla \cdot \mathbf{F} = \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} \]
\( F_1 = 2x^2y \), \( F_2 = yz^2 \), \( F_3 = z^3x \) について、それぞれの部分導関数を計算します。
- \( \frac{\partial F_1}{\partial x} = \frac{\partial}{\partial x}(2x^2y) = 4xy \)
- \( \frac{\partial F_2}{\partial y} = \frac{\partial}{\partial y}(yz^2) = z^2 \)
- \( \frac{\partial F_3}{\partial z} = \frac{\partial}{\partial z}(z^3x) = 3z^2x \)
したがって、
\[ \nabla \cdot \mathbf{F} = 4xy + z^2 + 3z^2x \]
3.2. 問題 2
ベクトル場 \( \mathbf{G}(x, y, z) = (G_1, G_2, G_3) \) のダイバージェンスを計算します。
- \( G_1 = e^x \sin(y) \), \( G_2 = x^2y \), \( G_3 = z^2 \cos(x) \)
それぞれの成分に対する偏微分を計算します。
- \( \frac{\partial G_1}{\partial x} = \frac{\partial}{\partial x}(e^x \sin(y)) = e^x \sin(y) \)
- \( \frac{\partial G_2}{\partial y} = \frac{\partial}{\partial y}(x^2y) = x^2 \)
- \( \frac{\partial G_3}{\partial z} = \frac{\partial}{\partial z}(z^2 \cos(x)) = 2z \cos(x) \)
したがって、ダイバージェンスは
\[ \nabla \cdot \mathbf{G} = e^x \sin(y) + x^2 + 2z \cos(x) \]
4. 応用例
4.1. ガウスの発散定理(ガウスの定理)
ガウスの発散定理は、ベクトル場のダイバージェンスを使って、閉じた表面上のフラックス(流束)と、表面が囲む体積内のダイバージェンスの積分の関係を示すものです。
\[ \oint_{\partial V} \mathbf{F} \cdot d\mathbf{A} = \int_{V} (\nabla \cdot \mathbf{F}) \, dV \]
ここで、
- \(\partial V\) は体積 \(V\) の境界(閉じた表面)
- \(d\mathbf{A}\) は表面要素ベクトル
- \(dV\) は体積要素
4.2. ラプラスの方程式
ラプラスの方程式は、スカラー場のラプラシアンがゼロである場合の関係式です。これはダイバージェンスを用いて表現されます。
\[ \nabla^2 \phi = 0 \]
ここで、\(\phi\) はスカラー場であり、\(\nabla^2\) はラプラシアン(ナブラのダイバージェンスと勾配の積)を意味します。
4.3. ポアソン方程式
ポアソン方程式は、スカラー場のラプラシアンがあるソース関数に等しい場合の関係式です。
\[ \nabla^2 \phi = f \]
ここで、\(\phi\) はスカラー場、\(f\) はソース関数です。
4.4. マクスウェルの方程式
マクスウェルの方程式の一部にはダイバージェンスが含まれます。
- ガウスの法則(電場):
\[ \nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0} \]
ここで、\(\mathbf{E}\) は電場、\(\rho\) は電荷密度、\(\epsilon_0\) は真空の誘電率。
- ガウスの法則(磁場):
\[ \nabla \cdot \mathbf{B} = 0 \]
ここで、\(\mathbf{B}\) は磁場。
これらの関係式を理解することで、ダイバージェンスの概念がどのように物理現象に応用されるかを深く理解できます。