ベクトルの共線条件と例題、連立方程式を利用しない解法について
1. 共線条件
$$\overrightarrow p =t \overrightarrow a + (1-t) \overrightarrow b$$
内分点の場合
$$\overrightarrow p = \frac{t \overrightarrow a + (1-t) \overrightarrow b}{1-t+t} = t \overrightarrow a + (1-t) \overrightarrow b$$
1.1. 共線条件の証明
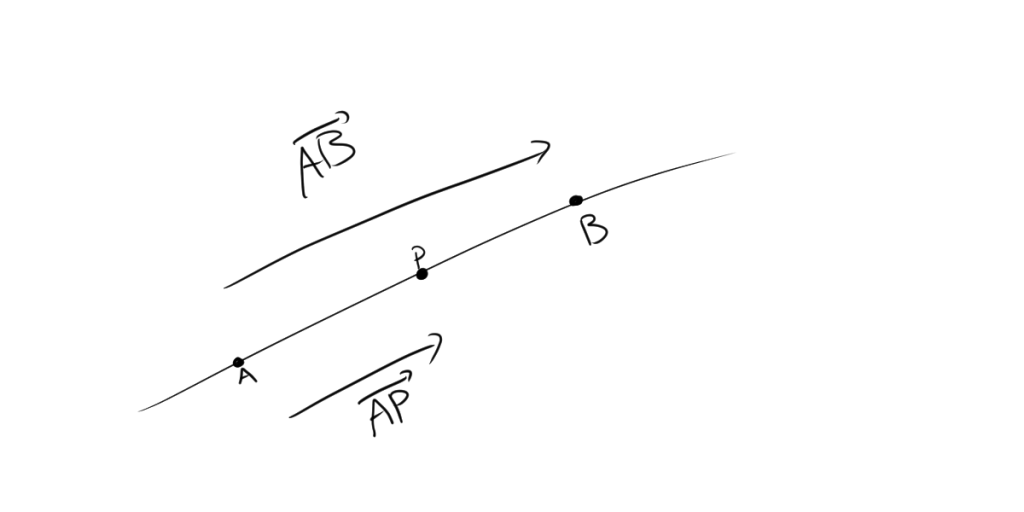
A,B,Pの位置ベクトルを$\overrightarrow a ,\overrightarrow b,\overrightarrow p $とすると、$\overrightarrow{AB}$と$\overrightarrow {AP}$は平行なベクトルであるので、tを実数とすると
$$\overrightarrow{AP}=t\overrightarrow {AB}$$
したがって、
$$\begin{align*} \overrightarrow{p} – \overrightarrow{a} &= t(\overrightarrow{b} – \overrightarrow{a}) \\ \overrightarrow{p} &= (1-t)\overrightarrow{a} + t\overrightarrow{b} \end{align*}$$
これは、$s+t=1$としたときに、
と表されることがある。
2. 共線の例題
2.1. 例題1
共線であるための条件として、ベクトル \( \overrightarrow{c} \) がベクトル \( \overrightarrow{a} \) と \( \overrightarrow{b} \) を実数tを利用して
\[ \overrightarrow{c} = t \overrightarrow{a} + (1 – t) \overrightarrow{b} \]
ベクトル \( \overrightarrow{a} \) と \( \overrightarrow{b} \) の各成分に対して、
\[ t(100, 0) + (1 – t)(50, 85) = (40, x) \]
各成分についての方程式を立てます。
\( x \) 成分に関して解くと、
\[ \begin{align*} 100t + 50 – 50t &= 40 \\ 50t + 50 &= 40 \\ 50t &= -10 \\ t &= -\frac{1}{5} \end{align*} \]
\( y \) 成分に関して解くと、
\[ \begin{align*} 85(1 – t) &= x \\ 85\left(1 + \frac{1}{5}\right) &= x \\ x &= 102 \end{align*} \]
\( t = -\frac{1}{5} \) を用いた結果、\( x = 102 \) となります。
2.2. 例題2
問題設定を図にすると
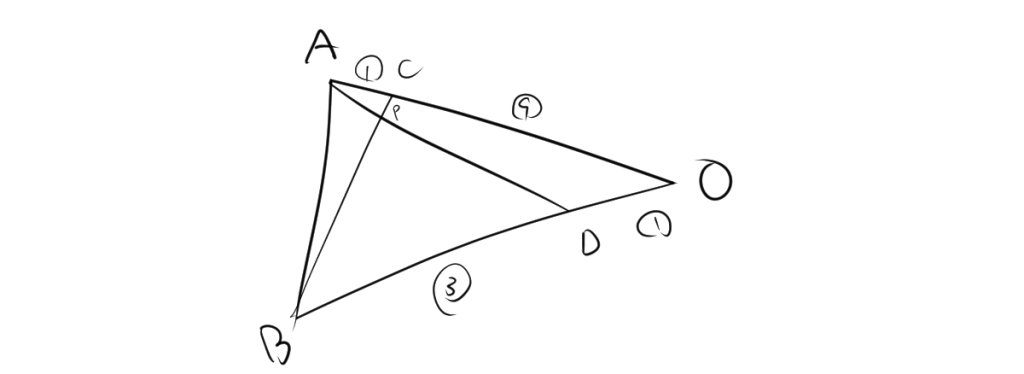$\overrightarrow {OA}= \overrightarrow a,\overrightarrow {OB} =\overrightarrow{b},\overrightarrow {OP} =\overrightarrow{p}$とする。
C,P,Bは共通の線分上に存在するので、実数tを用いて、
\[ \begin{align*} \overrightarrow{p} &= (1-t)\overrightarrow{OC} + t\overrightarrow{OB} \\ &= \frac{9}{10}(1-t)\overrightarrow{OA} + t\overrightarrow{OB} \\ &= \frac{9}{10}(1-t)\overrightarrow{a} + t\overrightarrow{b} \end{align*} \]
A,P,Dは共通の線分上に存在するので、実数sを用いて、
\[ \begin{align*} \overrightarrow{p} &= (1-s)\overrightarrow{OA} + s\overrightarrow{OD} \\ &= (1-s)\overrightarrow{OA} + \frac{s}{4}\overrightarrow{OB} \\ &= (1-s)\overrightarrow{a} + \frac{s}{4}\overrightarrow{b} \end{align*} \]
一次独立より、係数を比較すると、
$$\begin{cases} 1-s&=\frac{9}{10}(1-t)\\ s&=4t \end{cases}$$
$s=4t$を代入して計算すると、
\[ \frac{9}{10}(1-t) = 1 – 4t \] これを解くと、
\[ \begin{align*} 9(1 – t) &= 10(1 – 4t) \\ 9 – 9t &= 10 – 40t \\ 31t &= 1 \\ t &= \frac{1}{31} \end{align*} \]
\(s = 4t\) なので、 \[ s = 4 \times \frac{1}{31} = \frac{4}{31} \]
したがって、\(t = \frac{1}{31}\) および \(s = \frac{4}{31}\) となります。
よって、
\[ \begin{align*} \overrightarrow{p} &= \frac{9}{10}(1 – t)\overrightarrow{a} + t\overrightarrow{b} \\ &= \frac{9}{10} \cdot \frac{30}{31}\overrightarrow{a} + \frac{1}{31}\overrightarrow{b} \\ &= \frac{27}{31}\overrightarrow{a} + \frac{1}{31}\overrightarrow{b} \end{align*} \]
2.2.1. 連立方程式を利用しない解法
C,P,Bは共通の線分上に存在するので、実数tを用いて、
\[ \begin{align*} \overrightarrow{p} &= (1-t)\overrightarrow{OC} + t\overrightarrow{OB} \\ &= \frac{9}{10}(1-t)\overrightarrow{OA} + t\overrightarrow{OB} \\ &= \frac{9}{10}(1-t)\overrightarrow{OA} + 4t\overrightarrow{OD} \end{align*} \]
したがって、A,D,Pは共通の線分上に存在するため、係数の和が1になることから、
$$\frac{9}{10}(1-t)+4t = 1$$
次の方程式を解く際、両辺を 10 倍すると。
\[ \begin{align*} 9(1 – t) + 40t &= 10 \\ 9 – 9t + 40t &= 10 \\ 9 + 31t &= 10 \\ t &= \frac{1}{31} \end{align*} \]
あとは、先ほどと同様にtを代入して計算することでベクトルを求めることができる。
