【ベクトル解析】ベクトルの回転rotの意味と導出について

1. 回転(rot)とは
1.1. 定義
\[ \begin{align*} \text{rot}\ \mathbf{V} &= \nabla \times \mathbf{V} \\ &=\left( \frac{\partial V_z}{\partial y} – \frac{\partial V_y}{\partial z} \right) \vec{i} + \left( \frac{\partial V_x}{\partial z} – \frac{\partial V_z}{\partial x} \right) \vec{j} + \left( \frac{\partial V_y}{\partial x} – \frac{\partial V_x}{\partial y} \right) \vec{k} \\ &=\left( \frac{\partial V_z}{\partial y} – \frac{\partial V_y}{\partial z} ,\frac{\partial V_x}{\partial z} – \frac{\partial V_z}{\partial x} ,\frac{\partial V_y}{\partial x} – \frac{\partial V_x}{\partial y} \right) \end{align*} \]
ここで、\(\nabla\)(ナブラ)はベクトル微分演算子で、次のような形で書かれます。
\[ \nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) \]
\(\times\) はクロス積(外積)を表します。また、\(\vec{i}, \vec{j}, \vec{k}\) はそれぞれ \(x\), \(y\), \(z\) 軸方向の単位ベクトルです。rotはcurlという演算子で表されることがあります。
2. 回転の意味
2.1. 導出
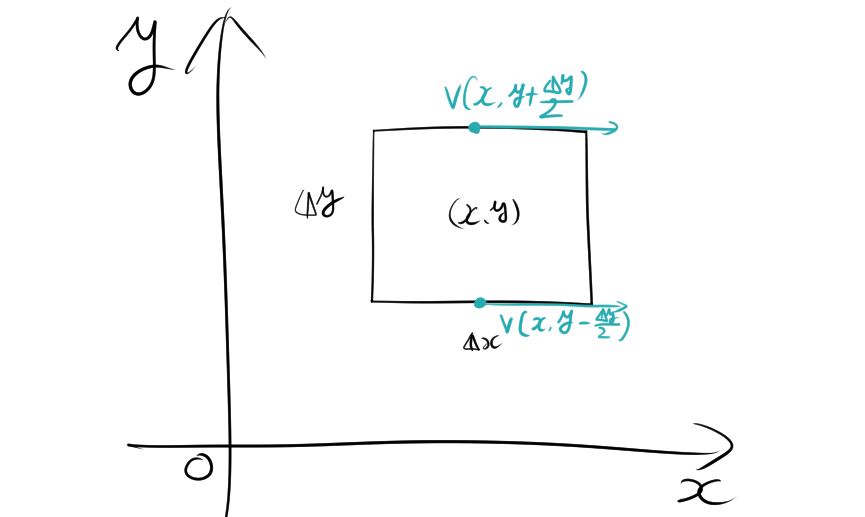
反時計回りを正とします。$(x, y)$を中心とする、\(\Delta x\) と \(\Delta y\) の長方形を考えます。
\[ V_x\left(x, y – \frac{\Delta y}{2}\right) – V_x\left(x, y + \frac{\Delta y}{2}\right) \]
$V_x$はVのx軸方向の成分であることを意味します。また、$\Delta x$だけベクトルがあるので、$\Delta y$だけのベクトルの大きさを考える必要があります。$\Delta x$は微小量であるので、すべて同じベクトルであると近似して\Delta xだけ掛けると
\[ \left\{V_x\left(x, y – \frac{\Delta y}{2}\right) – V_x\left(x, y + \frac{\Delta y}{2}\right)\right\} \Delta x \]
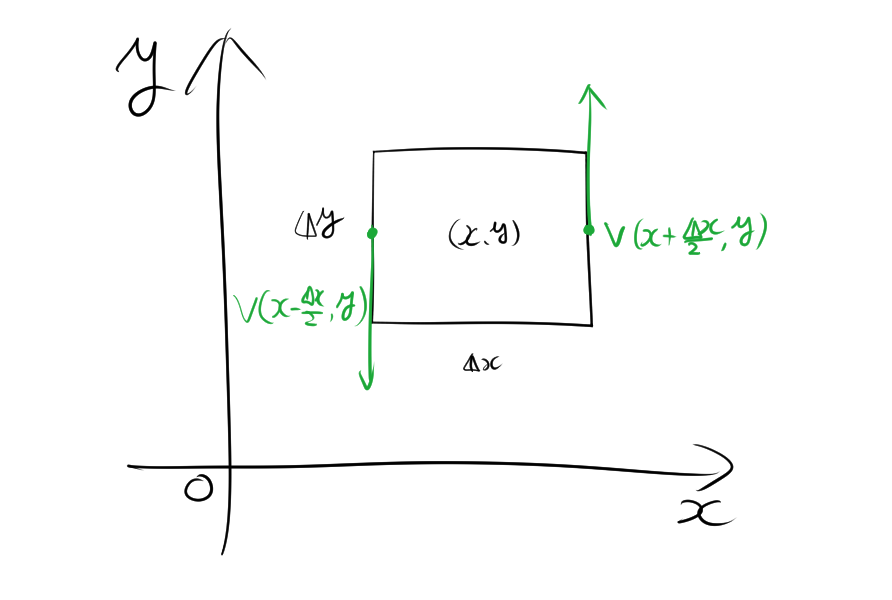
次に、y軸方向の回転に寄与する力は、
\[ V_y\left(x + \frac{\Delta x}{2}, y\right) – V_y\left(x – \frac{\Delta x}{2}, y\right) \]
$V_y$はVのy軸方向の成分であることを意味します。同様に、\(\Delta y\) も微小量であるため、近似的に回転に寄与する力は、
\[ \left\{V_y\left(x + \frac{\Delta x}{2}, y\right) – V_y\left(x – \frac{\Delta x}{2}, y\right)\right\} \Delta y \]
したがって、全体の回転に寄与する力の合計は次のように表すことができます。
\[ \left\{V_y\left(x, y – \frac{\Delta y}{2}\right) – V_y\left(x, y + \frac{\Delta y}{2}\right)\right\} \Delta x + \left\{V_x\left(x + \frac{\Delta x}{2}, y\right) – V_x\left(x – \frac{\Delta x}{2}, y\right)\right\} \Delta y \]
ここで、この式をテイラー展開すると、
\[ V_x\left(x + \frac{\Delta x}{2}, y\right) \approx V_x(x, y) + \frac{\partial V_x}{\partial x} \frac{\Delta x}{2}, \quad V_x\left(x – \frac{\Delta x}{2}, y\right) \approx V_x(x, y) – \frac{\partial V_x}{\partial x} \frac{\Delta x}{2} \]
同様に、
\[ V_y\left(x, y + \frac{\Delta y}{2}\right) \approx V_y(x, y) + \frac{\partial V_y}{\partial y} \frac{\Delta y}{2}, \quad V_y\left(x, y – \frac{\Delta y}{2}\right) \approx V_y(x, y) – \frac{\partial V_y}{\partial y} \frac{\Delta y}{2} \]
これらを代入して整理すると、次のようになります。
\[\left(-\frac{\partial V_x}{\partial y} + \frac{\partial V_y}{\partial x} \right)\Delta x\Delta y\]
今、仮想的に長方形を考えていた。しかし、$\Delta x\Delta y$を割ることで、面積によらない点における力の寄与を考えることができるので、
$$-\frac{\partial V_x}{\partial y} + \frac{\partial V_y}{\partial x}$$
となる。したがって、$\text{rot} \mathbf V$のz軸の成分であるので、今まで考えてきたことはz軸周りの回転であることがわかる。同様に、ほかの軸の成分も調べることができる。
2.2. 回転の意味
今回考えたベクトルの回転はxy平面上における回転のz軸成分を計算しており、この成分が非ゼロであれば、その場所でベクトル場が反時計回りの渦を巻いていることを意味します。
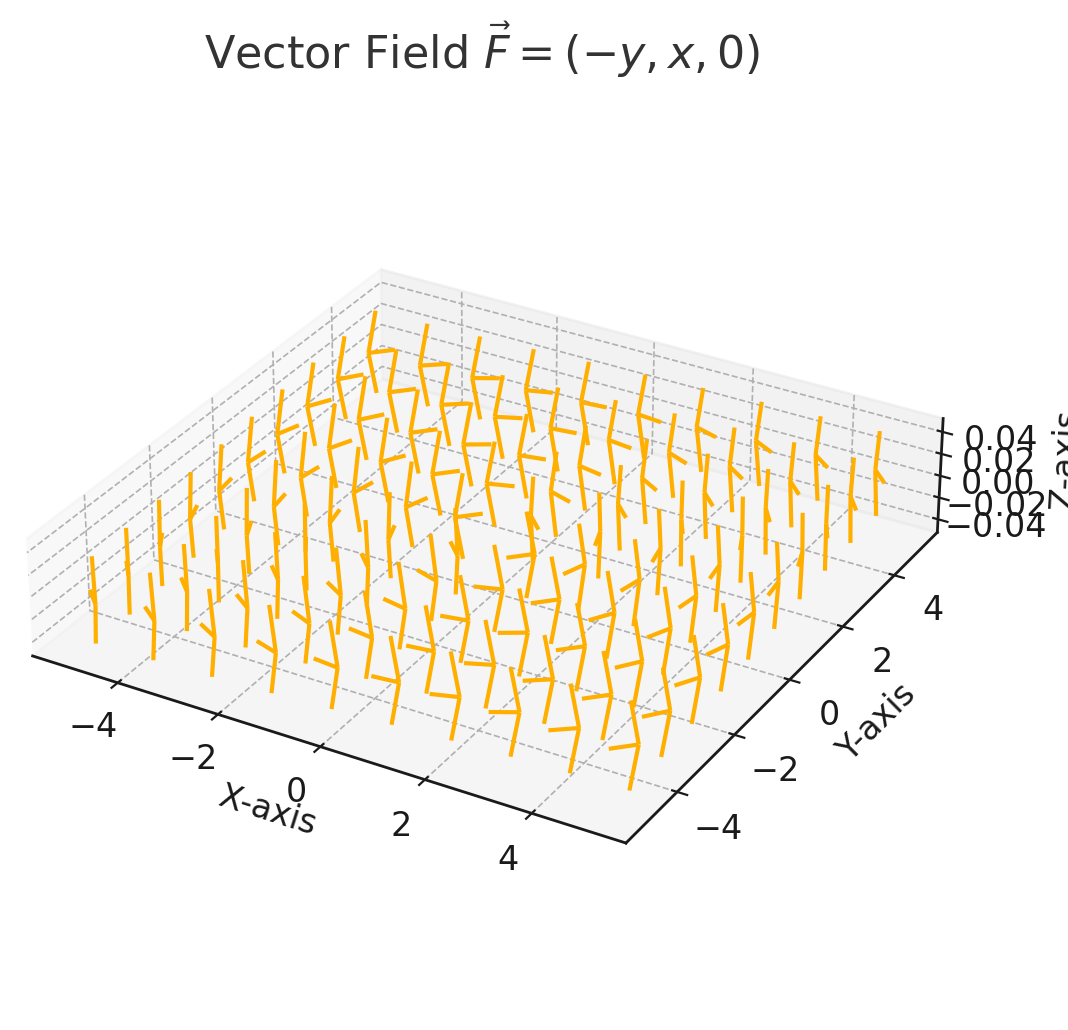
3. 例題
まず、\(\vec{F}\) の成分は以下の通りです。
- \(F_x = -y\)
- \(F_y = x\)
- \(F_z = 0\)
回転の各成分を計算します。
- \( \left( \frac{\partial F_z}{\partial y} – \frac{\partial F_y}{\partial z} \right) = \left( 0 – 0 \right) = 0 \)
- \( \left( \frac{\partial F_x}{\partial z} – \frac{\partial F_z}{\partial x} \right) = \left( 0 – 0 \right) = 0 \)
- \( \left( \frac{\partial F_y}{\partial x} – \frac{\partial F_x}{\partial y} \right) = \left( 1 – (-1) \right) = 2 \)
したがって、
\[ \text{rot}\ \vec{F} = (0, 0, 2) \]
この結果は、\(\vec{F}\) が \(z\) 軸周りに回転していることを示しています。