ベクトルのスカラーと平行なベクトル、成分の関係について

1. ベクトルとスカラー
ベクトルは、大きさと向きを持つ量です。例えば、2次元のベクトル \(\overrightarrow{{v}} = (x, y)\) は、座標平面上の点 \( (x, y) \) に向かう矢印として描かれます。
1.1. スカラー
スカラーとは、単に大きさ(数値)のみを持つ量です。ベクトルに対してスカラー倍をすると、そのベクトルの長さが変化し、向きが変わることもあります。
1.2. スカラー倍とベクトル
あるベクトル \(\overrightarrow{{v}} = (x, y)\) に対してスカラー \(k\) を掛ける操作をスカラー倍と言います。ベクトルの各成分に \(k\) を掛けることで、以下のようになります。
\[ k \overrightarrow{{v}} = (k \cdot x, k \cdot y) \]
例えば、\(\overrightarrow{{v}} = (2, 3)\) に対してスカラー \(k = 2\) を掛けると、スカラー倍後のベクトルは
\[ 2 \overrightarrow{{v}} = (2 \cdot 2, 2 \cdot 3) = (4, 6) \]
このように、スカラー倍をするとベクトルの向きはそのままで、長さが変化します。
2. 平行なベクトル
0ベクトルでない2つのベクトル \(\overrightarrow{{u}}\) と \(\overrightarrow{{v}}\) が平行であるとは、一方が他方のスカラー倍で表されるときです。
\[ \overrightarrow{{u}}と \overrightarrow{{v}}は平行 \Leftrightarrow \overrightarrow{{u}} = k \overrightarrow{{v}} \]
2.1. 証明
次の二つを証明します。
$$\overrightarrow{{u}}と \overrightarrow{{v}}は平行 \Rightarrow \overrightarrow{{u}} = k \overrightarrow{{v}}$$
$$\overrightarrow{{u}}と \overrightarrow{{v}}は平行 \Leftarrow \overrightarrow{{u}} = k \overrightarrow{{v}}$$
$ \Rightarrow $を証明します。 \(\overrightarrow{u}\) と \(\overrightarrow{v}\) が平行であると仮定します。平行であるということは、これらのベクトルが同じ方向、または反対方向を向いていることを意味します。したがって、ベクトルの大きさが同じか異なる場合があるので、1つのベクトルが他方のスカラー倍として表される。
$$\overrightarrow{{u}} = k \overrightarrow{{v}}$$
今度は逆に、$ \Leftarrow$を証明します。 \(\overrightarrow{u} = k \overrightarrow{v}\) が成立すると仮定します。このとき、ベクトル \(\overrightarrow{u}\) はベクトル \(\overrightarrow{v}\) のスカラー倍であり、ベクトルの大きさは異なりますが、\(\overrightarrow{u}\) と \(\overrightarrow{v}\) は同じ方向または反対方向を向いていることになります。したがって、\(\overrightarrow{u}\) と \(\overrightarrow{v}\) は平行であると言えます。
ベクトル \(\overrightarrow{u}\) と \(\overrightarrow{v}\) が平行であることは、あるスカラー \(k\) が存在して \(\overrightarrow{u} = k \overrightarrow{v}\) が成り立つことと同値です。
2.2. 例
- \(\overrightarrow{{u}} = (2, 4)\)
- \(\overrightarrow{{w}} = (-1, -2)\)
- \(\overrightarrow{{p}} = (3, 5)\)
\(\overrightarrow{{u}}\) は \(\overrightarrow{{v}}\) のスカラー倍 \(2 \overrightarrow{{v}} = (2 \cdot 1, 2 \cdot 2) = (2, 4)\) なので平行です。
\(\overrightarrow{{w}}\) はスカラー倍 \( -1 \overrightarrow{{v}} = (-1 \cdot 1, -1 \cdot 2) = (-1, -2)\) なので平行です。
\(\overrightarrow{{p}}\) はスカラー倍で表すことができないので、平行ではありません。
2.3. スカラー倍と反対向きのベクトル
スカラー \(k\) が負の値のとき、ベクトルの向きは反転します。例えば、スカラー \(k = -1\) を掛けると、ベクトルの向きが逆転し、長さは変わりません。
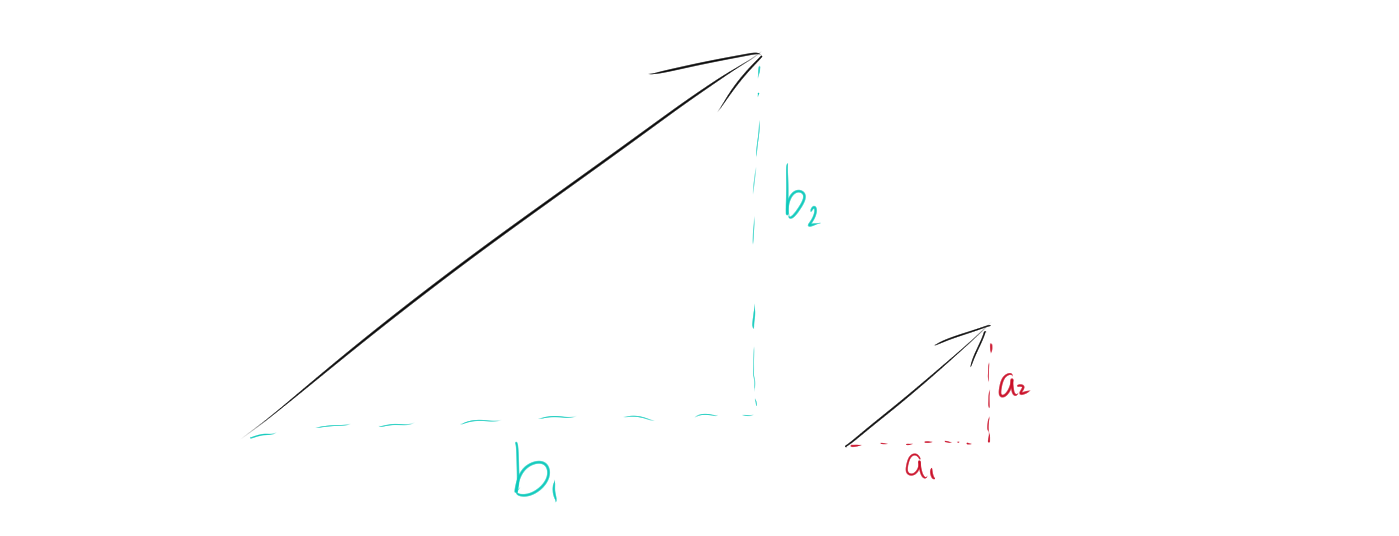
3. 平行なベクトルの成分の関係
$$a_1b_2-a_2b_1=0$$
が成り立つ。
例えば、次のように平行なベクトルがあるとする。
$$a_1:a_2=b_1:b_2$$
したがって、
$$a_1b_2-a_2b_1=0$$
が成り立つ。