ベクトルの大きさと単位ベクトルの計算方法と例題について

1. ベクトルの大きさとは?
ベクトルとは、大きさ(長さ)と向きを持った量のことです。平面上や空間で物体がどれだけの距離を移動するのか、どちらの方向に動いているのかなどを示すときに使います。
\[ |\vec{a}| = \sqrt{a_1^2 + a_2^2} \]
たとえば、ベクトル \(\vec{a} = (3, 4)\) の大きさを求めるとしましょう。この場合、
\[ |\vec{a}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
1.1. 3次元空間でのベクトルの大きさ
\[ |\vec{b}| = \sqrt{b_1^2 + b_2^2 + b_3^2} \]
例えば、ベクトル \(\vec{b} = (1, -2, 2)\) の場合、
\[ |\vec{b}| = \sqrt{1^2 + (-2)^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3 \]
となります。
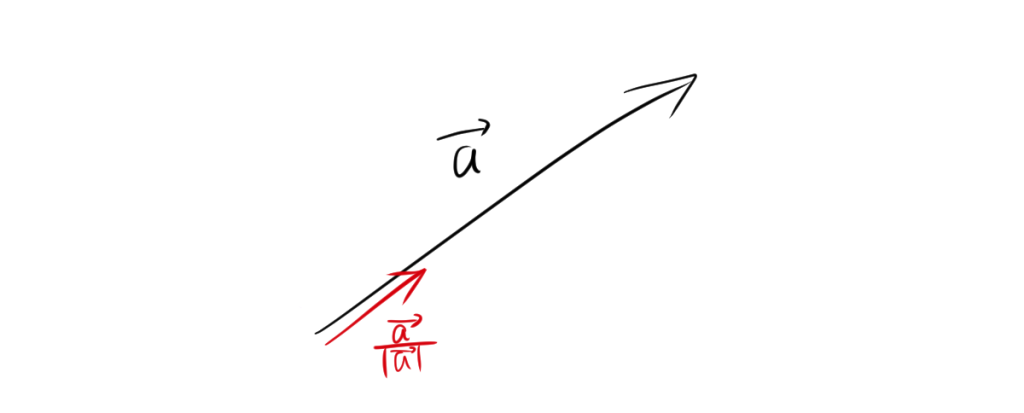
2. 単位ベクトルとは?
方向を変えずに大きさを1にすることで扱いやすくしています。
\[ \frac{\vec{a}}{|\vec{a}|} \]
つまり、元のベクトルをその大きさで割ることで、長さ1のベクトルを作るのです。このような操作を正規化といいます。
3. 例題
3.1. 例題1
まず、先ほど求めたようにベクトル \(\vec{a}\) の大きさは 5 です。したがって、単位ベクトルは
\[ \frac{\vec{a}}{|\vec{a}|} = \frac{(3, 4)}{5} = \left( \frac{3}{5}, \frac{4}{5} \right) \]
となります。
3.2. 例題2
ベクトル \(\vec{a} = (1, 2)\) と逆向きの単位ベクトルを求めるために、まずは \(\vec{a}\) の大きさを求め、その後、逆向きのベクトルを単位ベクトルにします。ベクトル \(\vec{a} = (1, 2)\) の大きさ \(|\vec{a}|\) は
\[ |\vec{a}| = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \]
ベクトル \(\vec{a}\) の逆向きのベクトルは \(-\vec{a} = (-1, -2)\) です。逆向きのベクトル \(-\vec{a}\) を単位ベクトルにするためには、その大きさで割ります。
\[ \frac{-\vec{a}}{|\vec{a}|} = \frac{(-1, -2)}{\sqrt{5}} = \left( -\frac{1}{\sqrt{5}}, -\frac{2}{\sqrt{5}} \right) \]
したがって、ベクトル \(\vec{a} = (1, 2)\) と逆向きの単位ベクトルは
\[ \left( -\frac{1}{\sqrt{5}}, -\frac{2}{\sqrt{5}} \right) \]