【直線・平面・円】ベクトル方程式と図形の表現について

ふゅか

ベクトル方程式について勉強しよう！直線のベクトル方程式って覚えてる？

はるか

うん、直線上の任意の点は \(\vec{r} = \vec{a} + t\vec{d}\) で表される。

1. ベクトルと直線の表現

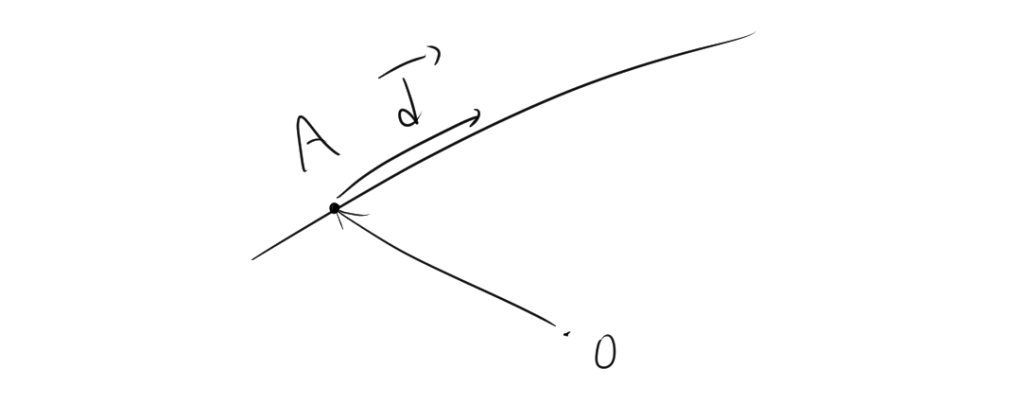
1.1. 直線のベクトル方程式

1.2. 直線の例

ふゅか

それじゃあ次、直線の具体的な例を見てみようか！点 \(A(1, 2)\) を通る直線の方程式、どうやって導くか説明できる？

はるか

ベクトル方程式から \(x\) と \(y\) の関係を整理するだけ。

点 \(A(1, 2)\) を通り、方向ベクトル \(\vec{d} = (3, 4)\) に沿う直線のベクトル方程式は

\[\begin{align*} \vec{r} &= (1, 2) + t(3, 4) \\ &= (3t+1,4t+2) \end{align*}\]

$\vec {r} =(x,y)$とすると、 $x=3t+1,y=4t+1$となる。ここから直線の方程式を求めることを考えます。$t=\dfrac{x-1}{3}$、$t=\dfrac{y-1}{4}$となるので、tを消去すると、

\[ \begin{align*} \dfrac{x-1}{3} &= \dfrac{y-1}{4} \\ 4(x – 1) &= 3(y – 1) \\ 4x – 4 &= 3y – 3 \\ 4x – 3y – 1 &= 0 \end{align*} \]

このように直線の方程式を求めることができます。

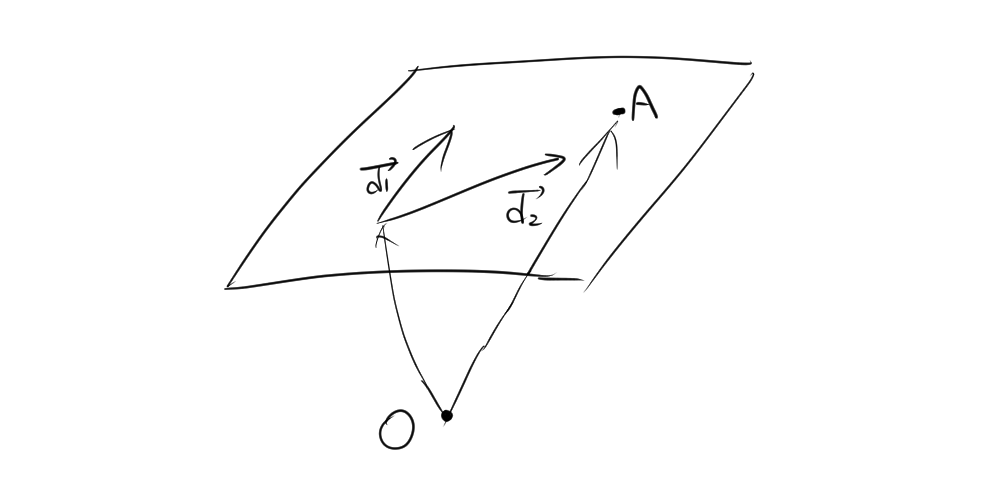
2. ベクトルによる平面の表現

ふゅか

次は平面の表現ね！直線と平面の違いって分かる？

はるか

平面は方向ベクトルが2本必要。直線は1本でいいけど。

2.1. 平面の例

点 \(A(1, 2,3)\) を通り、方向ベクトル \(\vec{d_1} = (4, 5,1)\) 、\(\vec{d_2} = (6, 7,1)\) に沿う直線のベクトル方程式は

\[\begin{align*} \vec{r} &= (1, 2,3) + t(3, 4,1)+s(6,7,1) \\ &=(1+3t+6s,2+4t+7s,3+t+s) \end{align*}\]

したがって、

$$x=1+3t+6s,\quad y=2+4t+7s,\quad z=3+s+t$$

となる。このように、パラーメータtで平面を表すことができました（媒介変数表示）。ここから、平面の方程式を導出してみましょう。

まず、\(z = 3 + t + s\) の式から、\(t\) を \(t = z – 3 – s\) と解きます。これを \(x\) および \(y\) の式に代入します。\(x\) の式に代入して、

\[ \begin{align*}x &= 1 + 3(z – 3 – s) + 6s \\ &= 1 + 3z – 9 – 3s + 6s \\ &= 3z – 8 + 3s \end{align*} \]

同様に、\(y\) の式に\(t = z – 3 – s\) を代入して、

\[ \begin{align*} y &= 2 + 4(z – 3 – s) + 7s \\ &= 2 + 4z – 12 – 4s + 7s \\ &= 4z – 10 + 3s \end{align*} \]

これで、\(x\) と \(y\) の式が次のようになりました。

\[ x = 3z – 8 + 3s,\quad y = 4z – 10 + 3s \]

これらの式から、\(s\) を消去すると、次のような関係が得られます。

\[ x – 3z + 8 = y – 4z + 10 \]

これを整理すると、

\[ x – y + z = 2 \]

3. ベクトルによる円の表現

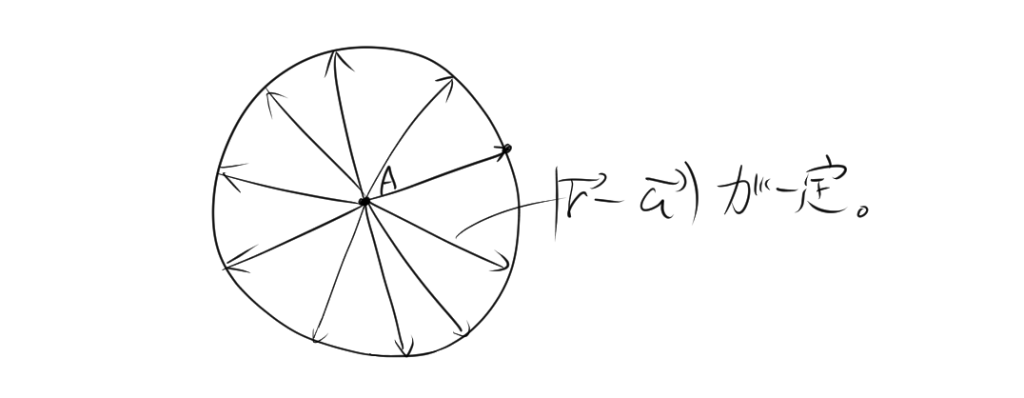
3.1.  円のベクトル方程式

円の中心の位置ベクトル \(\vec{a}\)、半径が \(r\) の円上の任意の点の位置ベクトル \(\vec{r}\) は、次の関係を満たします。

\[ |\vec{r} – \vec{a}| = r \]

ふゅか

それじゃあ、次に円のベクトル方程式を見てみよう！円の中心と半径を使ってどう表すか知ってる？

はるか

うん、中心からの距離が一定である位置ベクトルを考えることで表すことができる。

3.2. 円の例

中心が \( (2, 3) \)、半径が \(5\) の円を考えます。ベクトル方程式は次のようになります。

\[ |\vec{r} – (2, 3)| = 5 \]

ベクトル方程式を利用して円の方程式を求めます。$\vec{r}=(x,y)$とすると、

\[ \begin{align*} |\vec{r} – (2, 3)|^2 &= 25 \\ |\vec{r}|^2 – 2(2x + 3y) + 13 &= 25 \end{align*} \]

$|\vec{r} |^2=x^2+y^2$とすると、

\[ \begin{align*} x^2 + y^2 – 4x – 6y + 13 &= 25 \\ (x – 2)^2 – 4 + (y – 3)^2 – 9 + 13 &= 25 \\ (x – 2)^2 + (y – 3)^2 &= 25 \end{align*} \]