xの極限・微分・積分・グラフについて

ふゅか

ねぇ、ふゅか、今日は「関数 \( f(x) = x \) の極限・微分・積分・グラフ」について話すんだって！すごく基本的な関数だから、ちゃんと理解しておかないとね！

はるか

うん。シンプルだけど大事。

1. 極限

はるか

\( f(x) = x \) の極限は…簡単。\( x \to 0 \) のとき、関数は 0 に収束する。

ふゅか

そうだね！そして、\( x \to \infty \) のときは、関数も無限大に発散！逆に \( x \to -\infty \) のときは負の無限大になるよ〜。これで極限の基本はばっちり！

はるか

うん、簡単な直線の関数だし、極限もシンプル。

1.1. \( x \to 0 \) の極限

\[ \lim_{x \to 0} f(x) = \lim_{x \to 0} x = 0 \] 原点に向かうとき、関数 \( f(x) \) の値も 0 に収束します。

1.2. \( x \to \infty \) の極限

\[ \lim_{x \to \infty} f(x) = \infty \] \( x \) が無限に大きくなると、関数 \( f(x) \) も無限に発散します。

1.3. \( x \to -\infty \) の極限

\[ \lim_{x \to -\infty} f(x) = -\infty \] \( x \) が無限に小さくなると、関数 \( f(x) \) も負の無限に発散します。

2. 微分

したがって、関数 \( f(x) = x \) の導関数は \( 1 \) です。これは、直線 \( f(x) = x \) の傾きが常に \( 1 \) であることを意味します。

ふゅか

次は微分だね！直線の傾きを求めるって感じよね。

はるか

うん、\( f(x) = x \) の導関数は 1 だね。

ふゅか

そう！つまり、傾きが常に1！だから、どこを見ても一定の傾きで上昇するの♪

3. 積分

ここで、\( C \) は積分定数です。

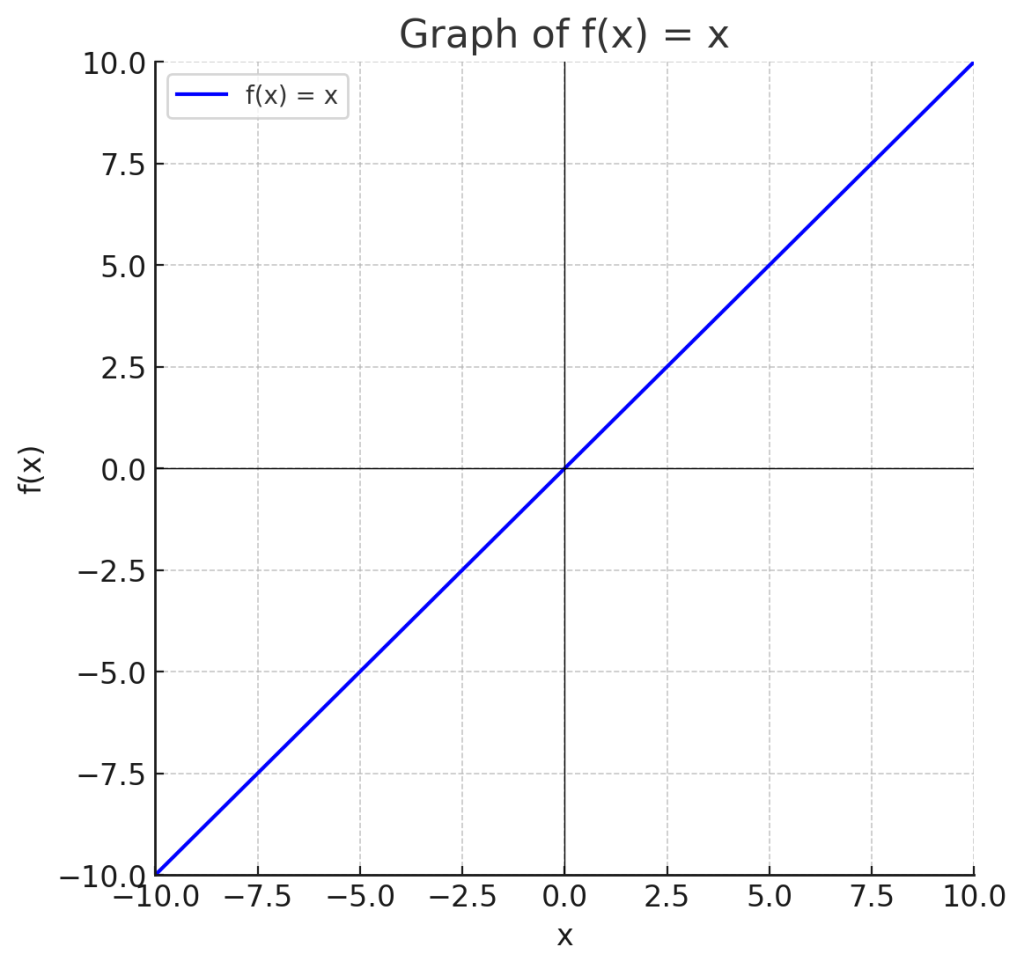
4. グラフ

4.1. 極値

関数 \( f(x) = x \) は一次関数です。一次関数を微分すると次のようになります。

\[ \frac{d}{dx} x = 1 \]

常に傾きが一定（今回の場合は \( 1 \)）であることがわかるため、変曲点や極値を持ちません。

極値とは、関数が最大値または最小値をとる点のことですが、一次関数のように直線で増加・減少し続ける場合、極値は存在しません。

そのため、関数 \( f(x) = x \) には極値がありません。

4.2. グラフ

関数 \( f(x) = x \) は、原点を通る傾き 1 の直線です。この直線は右上がりで、\( x \to \infty \) で発散し、\( x \to -\infty \) で負の無限大に向かって発散します。

ふゅか

そして、グラフ！原点を通る傾き1の直線だよね！右上がりで、ずーっと発散していく感じ。

はるか

うん、極値も変曲点もない。直線だから。