xe^xの極限・微分・積分・グラフについて

1. 極限

1.1. ${x \to 0}$の極限

\[ \lim_{x \to 0} x e^x = 0 \cdot e^0 = 0 \]

1.2. $x \to \infty$の極限

指数関数 \( e^x \) は非常に速く成長するので、無限大に発散します。

\[ \lim_{x \to \infty} x e^x = \infty \]

1.3. $x \to -\infty$の極限

指数関数 \( e^x \) は \( x \to -\infty \) で急激に 0 に近づきます。

したがって、
\[ \lim_{x \to -\infty} x e^x = 0 \]

2. 微分

関数 \( f(x) = x e^x \) の微分を計算すると、次のようになります。

\[ \frac{d}{dx} \left( x e^x \right) = \frac{d}{dx} \left( x \right) \cdot e^x + x \cdot \frac{d}{dx} \left( e^x \right) \]

\[ = e^x + x e^x \]

したがって、微分は

\[ f'(x) = e^x (1 + x) \]

 

3. 積分

関数 \( f(x) = x e^x \) の積分は、部分積分を用いて計算します。

部分積分で積分を計算すると次のようになります。

\[ \int x e^x dx = x e^x – \int e^x dx = x e^x – e^x + C = e^x (x – 1) + C \]

ここで、\( C \) は積分定数です。

4. グラフ

4.1. 極値

関数 \( f(x) = x e^x \) の極値を求めるために、まずはその導関数を求めます。

積の微分法則を用いると、次のようになります。

\[ f'(x) = \frac{d}{dx}(x e^x) = e^x + x e^x \]

これを整理すると、

\[ f'(x) = e^x(1 + x) \]

極値を求めるには、導関数が 0 になる点を探します。

\[ e^x(1 + x) = 0 \]

指数関数 \( e^x \) は常に正なので、\( 1 + x = 0 \) の場合に限って導関数は 0 になります。したがって、

\[ x = -1 \]

このとき、\( x = -1 \) で極値が存在することがわかります。

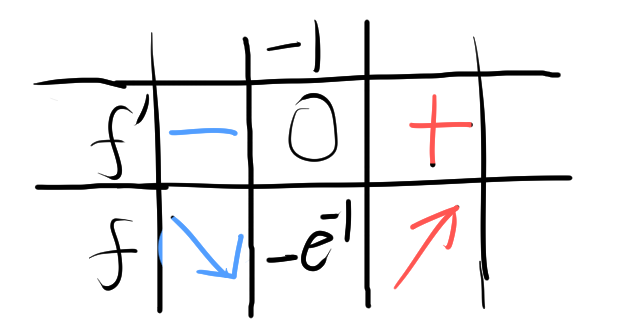
増減表を書くと次のようになります。

関数 \( f(x) = x e^x \) は、\( x = -1 \) で極小値を持ちます。

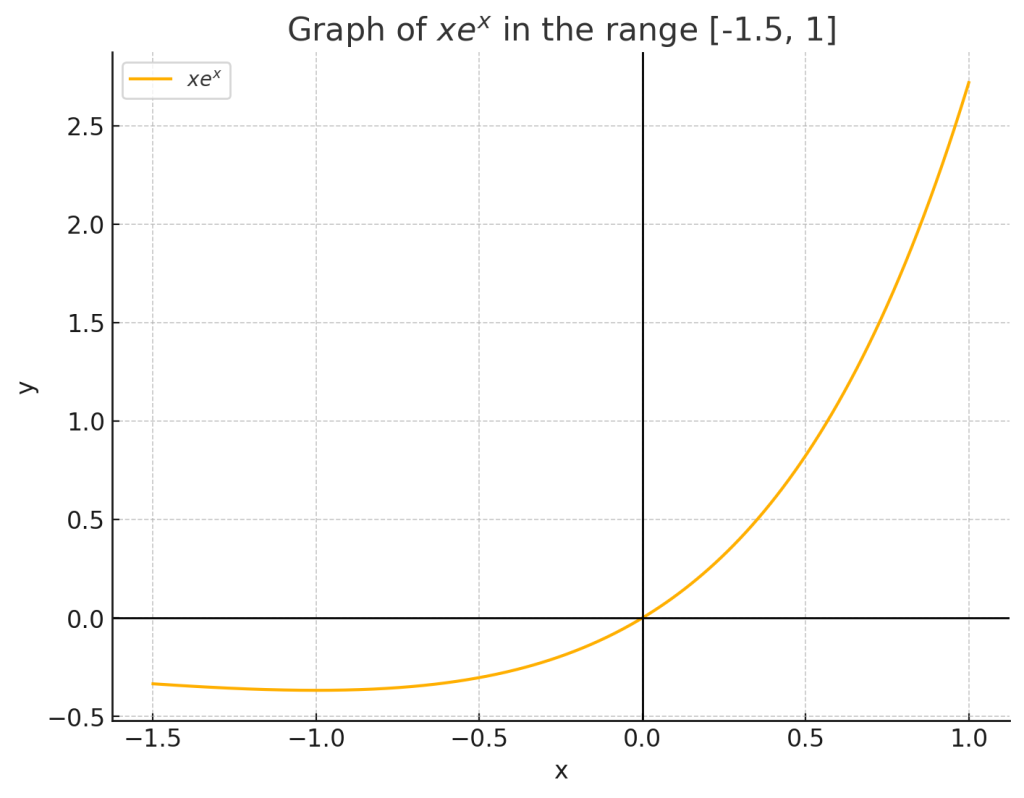
4.2. グラフ

極値を参考に、$xe^x$のグラフを見ると次のようになります。