xlogxの極限・微分・積分・グラフについて

1. 極限
1.1. 方法1($x=\frac{1}{t}$と置く)
$x=\frac{1}{t}$と置くと、\( t \to +\infty\)
\[ \lim_{x \to +0} x \log x \]
$$=\lim_{t \to +\infty}\frac{1}{t}\log \frac{1}{t}$$
$$=\lim_{t \to +\infty}\frac{-\log t}{t}=0$$
1.2. 方法2(ロピタルの定理を利用)
ロピタルの定理を利用すると、
\[ \lim_{x \to +0} x \log x \]
\[= \lim_{x \to +0} \frac{ \log x}{\frac{1}{x}} \]
\[= \lim_{x \to +0} \frac{ \frac{1}{x}}{\frac{-1}{x^2}} \]
\[= \lim_{x \to +0} -x =0 \]
2. 微分
\[ f'(x) = \frac{d}{dx} (x \log x) = \log x + 1 \]
\[ f”(x) = \frac{d}{dx} (\log x + 1) =\frac{1}{x}\]
2.1. グラフ
\( f(x) = x \log x \) のグラフは、\( x = 1 \) で 0 をります。\( x\to 0\)のとき 、グラフは 0 に近づきます。
増減表を書くと次のようになります。
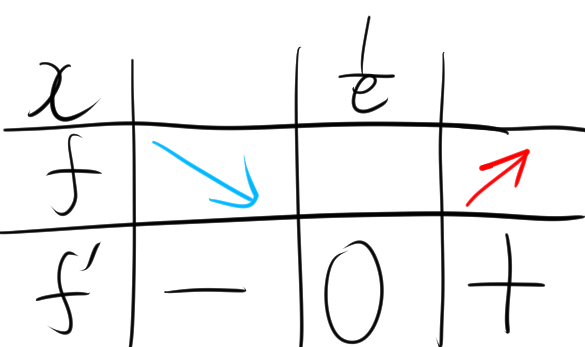
これらのことを踏まえてグラフを書くと次のようになります。
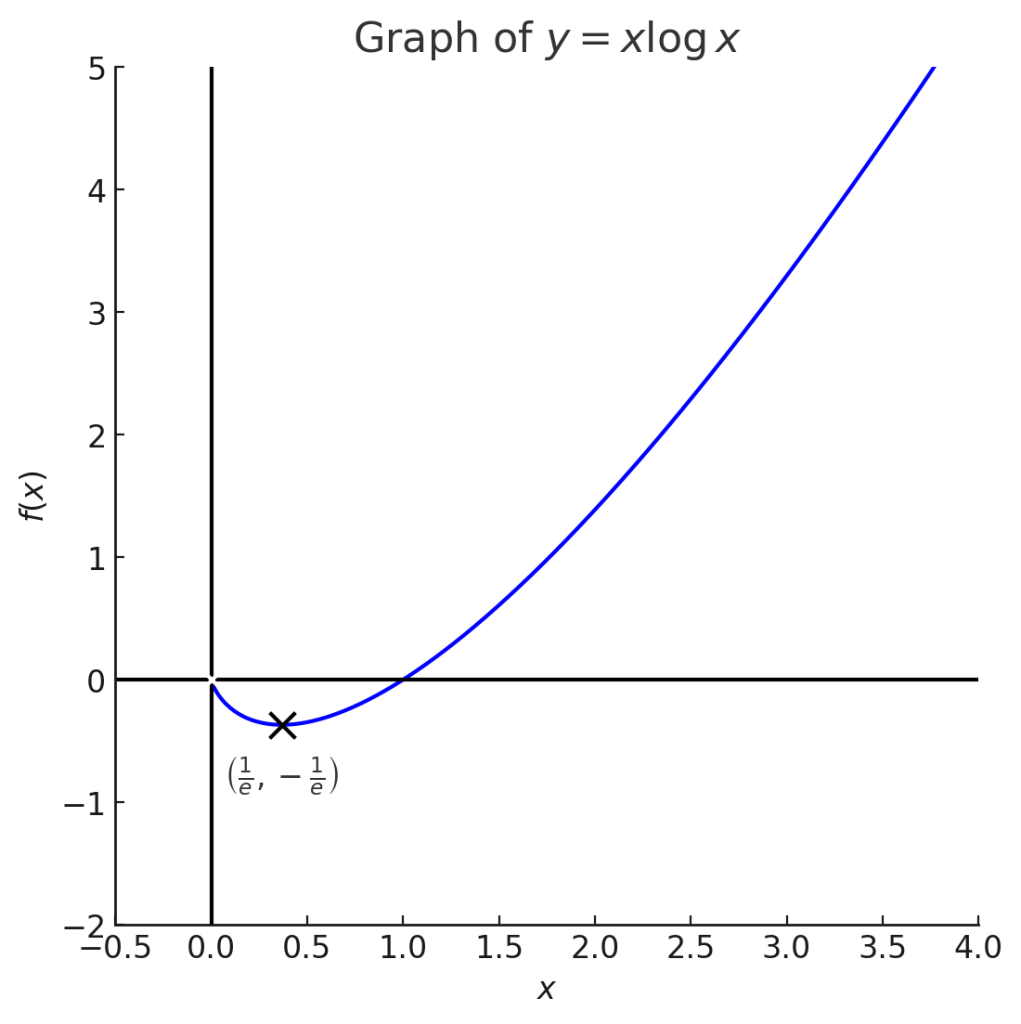
3. 積分
関数 \( f(x) = x \log x \) の不定積分を求めます。部分積分で計算すると、
\[ \int x \log x \, dx = \frac{x^2}{2} \log x – \int \frac{x^2}{2} \cdot \frac{1}{x} \, dx \]
\[ = \frac{x^2}{2} \log x – \int \frac{x}{2} \, dx \]
\[ = \frac{x^2}{2} \log x – \frac{x^2}{4} + C \]
この結果、不定積分は次のように表されます。
\[ \int x \log x \, dx = \frac{x^2}{2} \log x – \frac{x^2}{4} + C \]