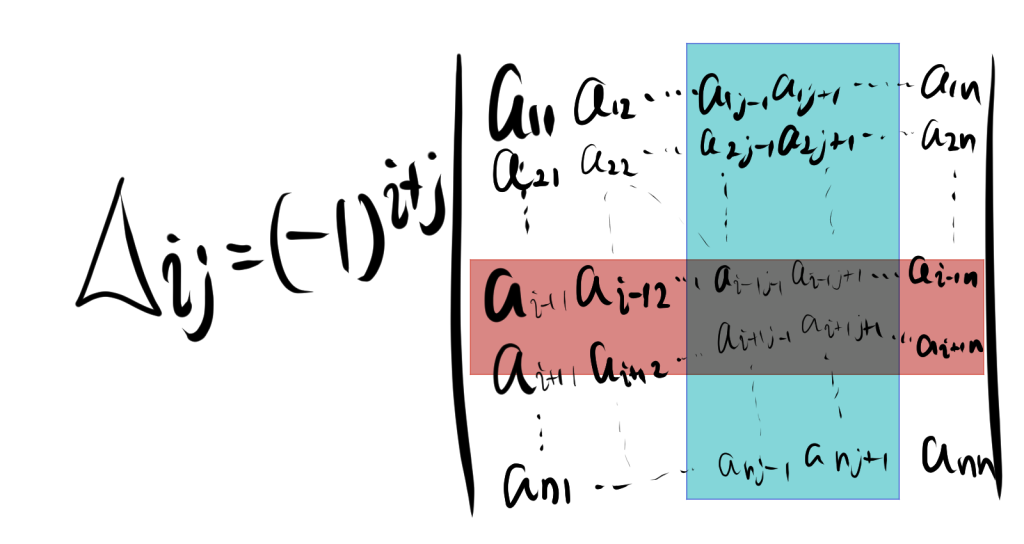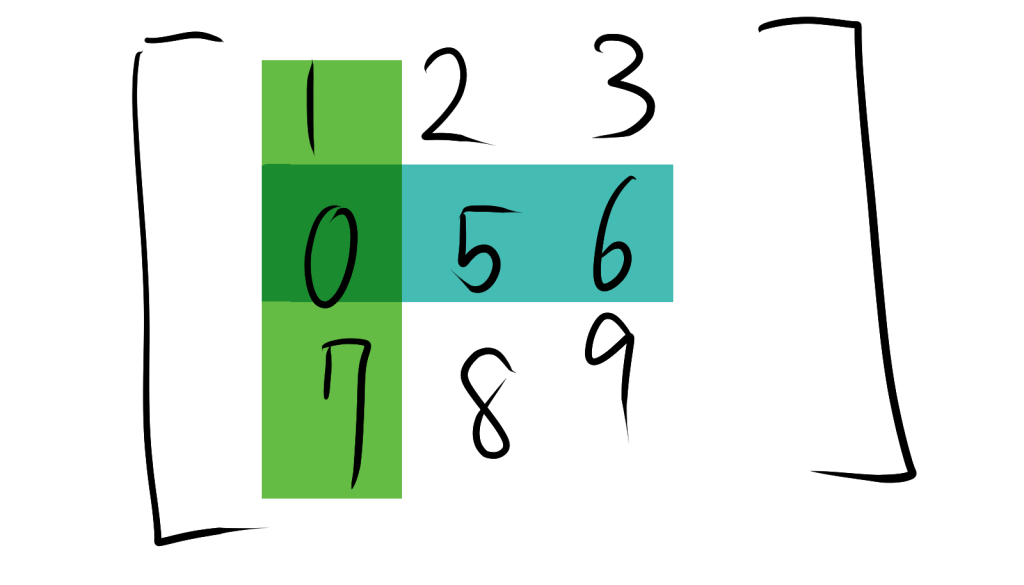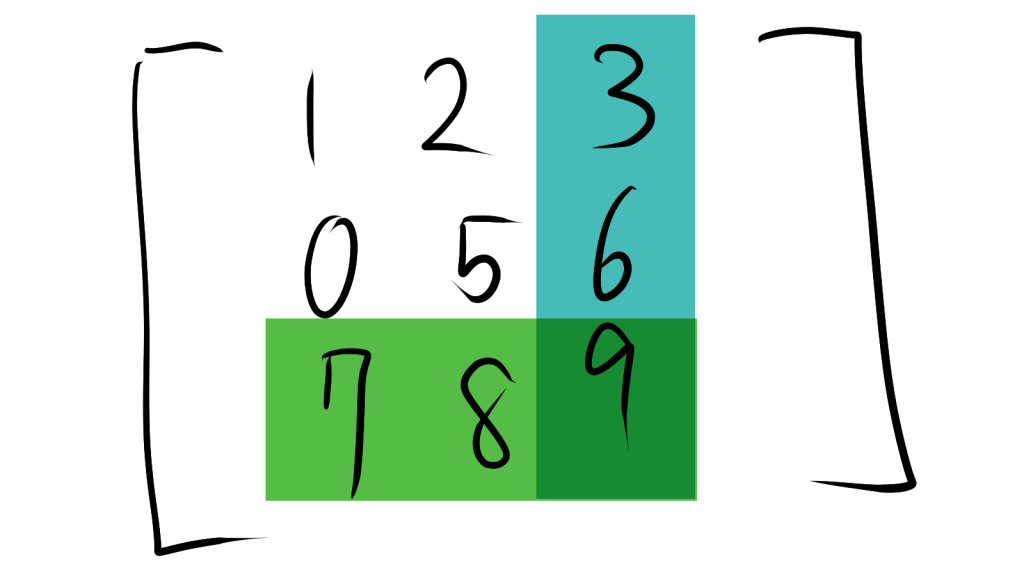【図解】余因子と余因子行列の定義・具体例・8つの性質・例題について

1. 余因子
余因子とは、ある行列の特定の要素を取り除いた部分行列の行列式に符号をつけたものです。具体的には、行列の各要素に対して、その要素を含む行と列を取り除いた部分行列を作成し、その部分行列の行列式に符号を付けることで余因子を計算します。
\[ \Delta_{ij} = (-1)^{i+j} |A_{ij}| \]
ここで、 \(|A_{ij}|\) は部分行列 \( A_{ij} \) の行列式を表し、 \( (-1)^{i+j} \) は余因子の符号を決定します。余因子の符号は \( i + j \) の合計が偶数の場合には正の符号になり、奇数の場合には負の符号になります。
- 余因子は、 \( \Delta_{ij} \) または \( \tilde{a}_{ij} \) と書かれます。
- 余因子は行列の逆行列を求める際や、行列式の展開に利用される重要な概念です。
1.1. 余因子の図解
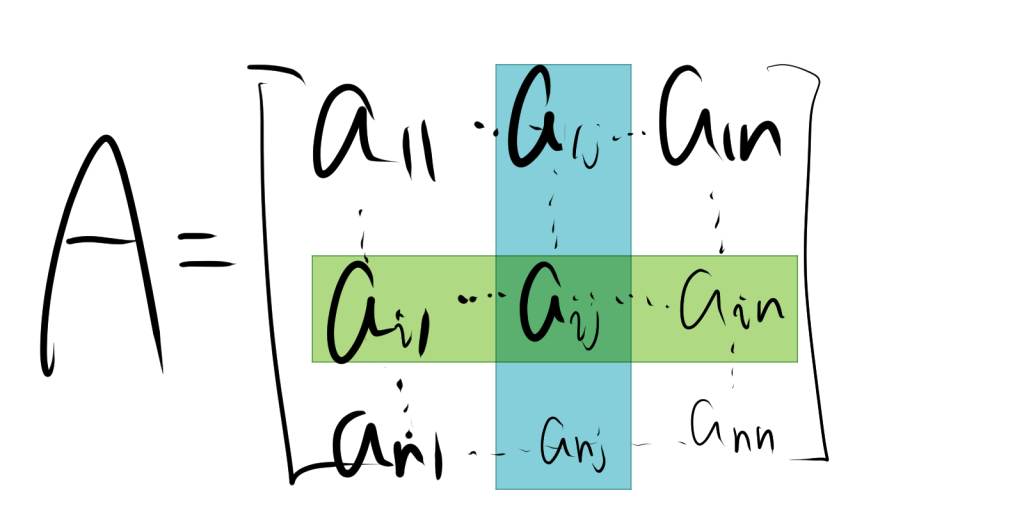
以上のn次の正方行列から色のついた部分を取り除いて、$i$行$j$列の余因子を図にすると以下のようになります。
色を付けた部分に注目してほしいのですが、$i$行目と$j$列目の成分が取り除かれていることが確認することができます。
1.2. 余因子の例題
$$A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}$$
行列Aの余因子$\Delta_{21},\Delta_{33}$を求めよ。
$A$ の$ (2,1) $要素の余因子を求める場合、$A$ の $2$行と $1$列目の要素を取り除いた以下の $2$次正方行列を考えます。
$A_{21} = \begin{bmatrix} 2 & 3 \\ 8 & 9 \\ \end{bmatrix}$
となるから、
$\Delta_{21}=(-1)^{2+1}\det A_{21}$
$=6$
$A$ の$ (3,3) $要素の余因子を求める場合、$A$ の $3$行と $3$列目の要素を取り除いた以下の $2$次正方行列を考えます。
$A_{33} = \begin{bmatrix} 1 & 2 \\ 0 & 5 \\ \end{bmatrix}$
となるから、
$\Delta_{33}=(-1)^{3+3}\det A_{33}$
$=5$
2. 余因子行列
余因子行列は、元の行列の各要素に対応する余因子を並べて構成した行列です。行列の要素を削除してできる小行列の行列式に符号をかけて得られるのが余因子であり、この余因子を元の行列の位置に配置したものが余因子行列となります。
\[ \mathrm{adj}(A) = \begin{bmatrix} \Delta_{11} & \Delta_{12} & \cdots & \Delta_{1n} \\ \Delta_{21} & \Delta_{22} & \cdots & \Delta_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \Delta_{n1} & \Delta_{n2} & \cdots & \Delta_{nn} \\ \end{bmatrix}^\top = \begin{bmatrix} \Delta_{11} & \Delta_{21} & \cdots & \Delta_{n1} \\ \Delta_{12} & \Delta_{22} & \cdots & \Delta_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ \Delta_{1n} & \Delta_{2n} & \cdots & \Delta_{nn} \\ \end{bmatrix} \]
- adjはアドジョイントと読みます
- $\mathrm{adj}(A)$は$\mathrm{cof}(A)$、$\widetilde {A}$とも書かれます。
- 余因子行列は古典随伴行列とも呼ばれます。
3. 余因子行列の性質
3.1. 逆行列との関係
\[ A^{-1} = \frac{1}{\det(A)} \text{adj}(A) \]
$\frac{1}{\det(A)} \text{adj}(A)$を計算します。
$$A \frac{1}{\det(A)} \text{adj}(A) = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} \cdots & a_{nn} \end{bmatrix} \frac{1}{\det(A)} \begin{bmatrix} \Delta_{11} & \Delta_{21} & \cdots & \Delta_{n1} \\ \Delta_{12} & \Delta_{22} & \cdots & \Delta_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ \Delta_{1n} & \Delta_{2n} & \cdots & \Delta_{nn} \\ \end{bmatrix}$$
ここで、$A \frac{1}{\det(A)} \text{adj}(A) $の(i,j)の要素を$c_{ij}$と置きます。
$$c_{ij}=\frac{1}{\det(A)}\sum_{k=1}^{n} a_{ik}\Delta_{jk}$$
[1]$i=j$の場合、
$$c_{ii}=\frac{1}{\det(A)}\sum_{k=1}^{n} a_{ik}\Delta_{ik}$$
となるため、$c_{ii}$は行列Aの余因子展開であるため、
$$c_{ii}=\frac{1}{\det(A)}\det(A)=1$$
[2]$i \neq j$の場合、
$$c_{ij}=\frac{1}{\det(A)}\sum_{k=1}^{n} a_{ik}\Delta_{jk}$$
となるため、$\sum_{k=1}^{n} a_{ik}\Delta_{jk}$はj行目の余因子展開を行った結果と考えられる。したがって、j行目の要素がi行目と同じであると考えられるため、
$$\sum_{k=1}^{n} a_{ik}\Delta_{jk} = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} = 0 $$
以上より、$A \frac{1}{\det(A)} \text{adj}(A) $は単位行列になる。したがって、$\frac{1}{\det(A)} \text{adj}(A)$は$A$の逆行列になる。
$$A^{-1} = \frac{1}{\det(A)} \text{adj}(A) $$
3.2. 行列式との関係
\[ A \widetilde A = \widetilde A A = \det(A) I_n \]
ここで、\( \det(A) \) は行列 \( A \) の行列式、\( I_n \) は \( n \times n \) の単位行列です。
行列 \( A \) の逆行列 \( A^{-1} \) が存在する場合、次の式が成り立ちます。
\[ A^{-1} = \frac{1}{\det(A)} \widetilde{A}, \]
ここで、\( \widetilde{A} \) は \( A \) の余因子行列です。
逆行列の定義により、次の関係が成り立ちます。
\[ A A^{-1} = A^{-1} A = I_n, \]
これを書き換えると、
\[ A \left( \frac{1}{\det(A)} \widetilde{A} \right) = \left( \frac{1}{\det(A)} \widetilde{A} \right) A = I_n. \]
この式を整理すると、
\[ \frac{1}{\det(A)} A \widetilde{A} = \frac{1}{\det(A)} \widetilde{A} A = I_n. \]
両辺に \( \det(A) \) を掛けると、
\[ A \widetilde{A} = \widetilde{A} A = \det(A) I_n. \]
これで、行列 \( A \) の余因子行列 \( \widetilde{A} \) を使った式 \( A \widetilde{A} = \widetilde{A} A = \det(A) I_n \) が成り立つことが証明されました。
3.3. 転置との関係
\[ (\text{adj}(A))^\top = \text{adj}(A^\top ) \]
つまり、余因子行列を転置しても、それは元の行列の転置の余因子行列と同じになります。
まず、余因子行列 \(\text{adj}(A)\) の定義を確認します。
行列 \( A \) の余因子行列は、各成分が \( A \) の対応する小行列式の余因子で構成される行列です。
行列 \( A \) の \( (i, j) \) 成分の余因子を \( \Delta_{ij} \) とすると、余因子行列 \( \text{adj}(A) \) は次のように定義されます。
\[ \text{adj}(A) = \begin{bmatrix} \Delta_{11} & \Delta_{12} & \cdots & \Delta_{1n} \\ \Delta_{21} & \Delta_{22} & \cdots & \Delta_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \Delta_{n1} & \Delta_{n2} & \cdots & \Delta_{nn} \end{bmatrix} \]
行列 \( A \) の転置 \( A^\top \) の \( (i, j) \) 成分の余因子を求めます。
行列 \( A^\top \) の \( (i, j) \) 成分の余因子は、元の行列 \( A \) の \( (j, i) \) 成分の余因子に対応します。
すなわち、\( A^\top \) の \( (i, j) \) 成分の余因子は \( \Delta_{ji} \) です。
したがって、転置行列 \( A^\top \) の余因子行列 \( \text{adj}(A^\top) \) は次のように表されます。
\[ \text{adj}(A^\top) = \begin{bmatrix} \Delta_{11} & \Delta_{21} & \cdots & \Delta_{n1} \\ \Delta_{12} & \Delta_{22} & \cdots & \Delta_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ \Delta_{1n} & \Delta_{2n} & \cdots & \Delta_{nn} \end{bmatrix} \]
今度は、余因子行列 \( \text{adj}(A) \) を転置します。
\[ (\text{adj}(A))^\top = \begin{bmatrix} \Delta_{11} & \Delta_{21} & \cdots & \Delta_{n1} \\ \Delta_{12} & \Delta_{22} & \cdots & \Delta_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ \Delta_{1n} & \Delta_{2n} & \cdots & \Delta_{nn} \end{bmatrix} \]
これでわかるように、\( (\text{adj}(A))^\top \) と \( \text{adj}(A^\top ) \) は同じ行列です。
したがって、
\[ (\text{adj}(A))^\top = \text{adj}(A^\top ) \]
が成立することが示されました。
3.4. 行列積との分配法則
\[ \text{adj}(AB) = \text{adj}(B) \text{adj}(A) \]
行列 \( AB \) に対して、
\[ AB \cdot \text{adj}(AB) = \det(AB) I \]
となります。まずは$AB \cdot \text{adj}(B) \text{adj}(A)$を考えます。余因子行列の性質を利用して、以下のように変形します。
$$AB \cdot \text{adj}(B) \text{adj}(A)$$
$$=A(B \cdot \text{adj}(B)) \text{adj}(A)$$
\[ = A(\det(B) I) \text{adj}(A) \]
\[ = \det(B) (A \cdot \text{adj}(A)) \]
\[ = \det(B) (\det(A) I) \]
\[ = \det(A) \det(B) I \]
$$ = AB \cdot \text{adj}(AB)$$
これにより、
\[ AB \cdot \text{adj}(AB) = AB \cdot \text{adj}(B) \text{adj}(A) \]
両辺に \( (AB)^{-1} \)を右からかけると、これらの行列が等しいことが示されます。
\[ \text{adj}(AB) = \text{adj}(B) \text{adj}(A) \]
3.5. スカラー倍
\[ \text{adj}(cA) = c^{n-1} \text{adj}(A) \]
ここで \( n \) は行列 \( A \) のサイズ(次元)です。
スカラー \( c \) を掛けた行列 \( cA \) の余因子行列 \( \text{adj}(cA) \) を考えます。この行列について
\[ (cA) \cdot \text{adj}(cA) = \det(cA) I_n \]
が成り立ちます。ここで、行列のスカラー倍の行列式の性質より、
\[ \det(cA) = c^n \det(A) \]
となるため、上の式は次のように書けます。
\[ cA \cdot \text{adj}(cA) = c^n \det(A) I_n \]
次に、行列 \( A \) の余因子行列 \( \text{adj}(A) \) を使って、スカラー倍 \( c \) の行列 \( cA \) の余因子行列を表現します。\( \text{adj}(A) \) と \( A \) との関係式をスカラー \( c \) で変形します。
\[ c \left( A \cdot \text{adj}(A) \right) = c \det(A) I_n \]
となり、さらにこれを \( c^{n-1} \) 倍します。
\[ cA \cdot c^{n-1} \text{adj}(A) = c^n \det(A) I_n \]
ここで、\( cA \cdot \text{adj}(cA) = c^n \det(A) I_n \) と \( cA \cdot c^{n-1} \text{adj}(A) = c^n \det(A) I_n \) がともに \( cA \) の行列積として等しいため、
$$cA \cdot \text{adj}(cA) = cA \cdot c^{n-1} \text{adj}(A) $$
\[ \text{adj}(cA) = c^{n-1} \text{adj}(A) \]
が成立します。
3.6. 余因子行列の行列式
$$\det(\operatorname{adj}(A))=(\det A)^{n-1}$$
である。
\(\det(A \cdot \operatorname{adj}(A)) = \det((\det A) I_n)\) であるため、
\[ \det(A \cdot \operatorname{adj}(A)) = (\det A)^n \]
一方で、行列式の性質から
\[ \det(A \cdot \operatorname{adj}(A)) = \det(A) \cdot \det(\operatorname{adj}(A)) \]
なので、
\[ \det(A) \cdot \det(\operatorname{adj}(A)) = (\det A)^n \]
上記の式を \( \det(A) \) で割ると、
\[ \det(\operatorname{adj}(A)) = \frac{(\det A)^n}{\det A} = (\det A)^{n-1} \]
3.7. 行列のべき乗と余因子行列
\[ \text{adj}(A^k) = (\text{adj}(A))^k \]
まず、行列 \( A \) の累乗 \( A^k \) に対して随伴行列を求めます。
\[ \text{adj}(A^k) = \text{adj}(A \cdot A^{k-1}) \]
\(\text{adj}(A \cdot B) = \text{adj}(B) \text{adj}(A)\) を利用して、
\[ \text{adj}(A^k) = \text{adj}(A^{k-1}) \text{adj}(A) \]
同様にして、\(\text{adj}(A^{k-1})\) を展開していきます。
\[ \text{adj}(A^{k-1}) = \text{adj}(A^{k-2}) \text{adj}(A) \]
したがって、
\[ \text{adj}(A^k) = \text{adj}(A^{k-2}) \text{adj}(A) \text{adj}(A) \]
この手順を繰り返すと、
\[ \text{adj}(A^k) = \text{adj}(A) \cdot \text{adj}(A) \cdot \ldots \cdot \text{adj}(A)\]
したがって、最終的に
\[ \text{adj}(A^k) = (\text{adj}(A))^k \]
これで、\(\text{adj}(A^k) = (\text{adj} A)^k\) が成立することが示されました。
3.8. 行列の等式
\[ A \operatorname{adj}(A+B)B = B \operatorname{adj}(A+B)A \]
\( A \operatorname{adj}(A + B)B \) と \( B \operatorname{adj}(A + B)A \) が等しいことを示すために、まず左辺を展開します。
\[ A \operatorname{adj}(A + B)B = (A + B – B) \operatorname{adj}(A + B)B \] \[ = (A + B) \operatorname{adj}(A + B)B – B \operatorname{adj}(A + B)B \]
\((A + B) \operatorname{adj}(A + B) = \det(A + B) I\) なので、
\[ = \det(A + B) B – B \operatorname{adj}(A + B)B \]
\( B \operatorname{adj}(A + B)A \) も同様に展開します。
\[ B \operatorname{adj}(A + B)A = B \operatorname{adj}(A + B)(A + B – B) \]
\[ = B \operatorname{adj}(A + B)(A + B) – B \operatorname{adj}(A + B)B \]
\[ = \det(A + B) B – B \operatorname{adj}(A + B)B \]
左辺と右辺を比較すると、どちらも \[ \det(A + B) B – B \operatorname{adj}(A + B)B \] となり、したがって \[ A \operatorname{adj}(A + B)B = B \operatorname{adj}(A + B)A \] という等式が成り立つことが示されました。
4. 余因子行列の例題
$$A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}$$
とする。行列$A$の$\mathrm{adj(A)}$を求めよ。
まず、余因子を求める。
$$\Delta_{11} = \begin{vmatrix} 5 & 6 \\ 8 & 9 \end{vmatrix} = -3$$
$$\Delta_{12} = -\begin{vmatrix} 0 & 6 \\ 7 & 9 \end{vmatrix} = 42$$
$$\Delta_{13} = \begin{vmatrix} 0 & 5 \\ 7 & 8 \end{vmatrix} = -35$$
$$\Delta_{21} = -\begin{vmatrix} 2 & 3 \\ 8 & 9 \end{vmatrix} = 6$$
$$\Delta_{22} = \begin{vmatrix} 1 & 3 \\ 7 & 9 \end{vmatrix} = -12$$
$$\Delta_{23} = -\begin{vmatrix} 1 & 2 \\ 7 & 8 \end{vmatrix} = 6$$
$$\Delta_{31} = \begin{vmatrix} 2 & 3 \\ 5 & 6 \end{vmatrix} = -3$$
$$\Delta_{32} = -\begin{vmatrix} 1 & 3 \\ 0 & 6 \end{vmatrix} = -6$$
$$\Delta_{33} = \begin{vmatrix} 1 & 2 \\ 0 & 5 \end{vmatrix} = 5$$
最後に余因子行列$\mathrm{adj(A)}$を求めると、
$$\mathrm{adj(A)}=\begin{bmatrix}-3 & 6 & -3\\42 & -12 & -6\\ -35 & 6 &5\\ \end{bmatrix}$$
となる。