ヤングの不等式(Young's inequality)の証明と意味について

1. ヤングの不等式とは?
\(a, b > 0\) であるとき、ヤングの不等式は、以下の形で表されます。
\[ ab \leq \frac{a^p}{p} + \frac{b^q}{q} \]
ここで、\(p, q > 1\) の間には次の関係が成り立ちます。
\[ \frac{1}{p} + \frac{1}{q} = 1 \]
1.1. ヤングの不等式の特別な場合
特にシンプルな例として、\(p = q = 2\) の場合を考えると、不等式は以下のように簡略化されます。
\[ ab \leq \frac{a^2}{2} + \frac{b^2}{2} \]
これは高校数学でよく知られる「相加相乗平均の不等式」になります。
2. イェンセンの不等式を用いた証明
凸関数で成り立つイェンセンの不等式を利用して、ヤングの不等式を証明します。イェンセンの不等式は、凸関数に対して次の不等式が成り立ちます。
\[ \lambda f(x) + (1-\lambda) f(y) \geq f(\lambda x + (1-\lambda)y) \] (ここで、\(\lambda \in [0, 1]\))
\(f(x) = e^x\) は、$f^{\prime\prime}(x)>0$であるので、凸関数である。したがって、イェンゼンの不等式より、\(\lambda \in [0, 1]\)とすると、
\[ \lambda f(x) + (1-\lambda) f(y) \geq f(\lambda x + (1-\lambda)y) \]
ここで、
\[ \frac{1}{p} + \frac{1}{q} = 1 \]
という関係が成り立っているので、\(\lambda = \frac{1}{p}\)、\(1-\lambda = \frac{1}{q}\) と置くことができるので、
\[ \frac{f(x)}{p} + \frac{f(y)}{q} \geq f\left(\frac{x}{p}+\frac{y}{q} \right) \]
つまり、
\[ \frac{e^x}{p} + \frac{e^y}{q} \geq e^{\frac{x}{p}}e^{\frac{y}{q} } \]
$a=e^{\frac{x}{p}},b=e^{\frac{y}{q} }$ としたとき、次のようにヤングの不等式の形になる。
\[ \frac{a^p}{p} + \frac{b^q}{q} \geq ab \]
3. ヤングの不等式の積分形
ヤングの不等式は次のように、積分の形で表すことができます。
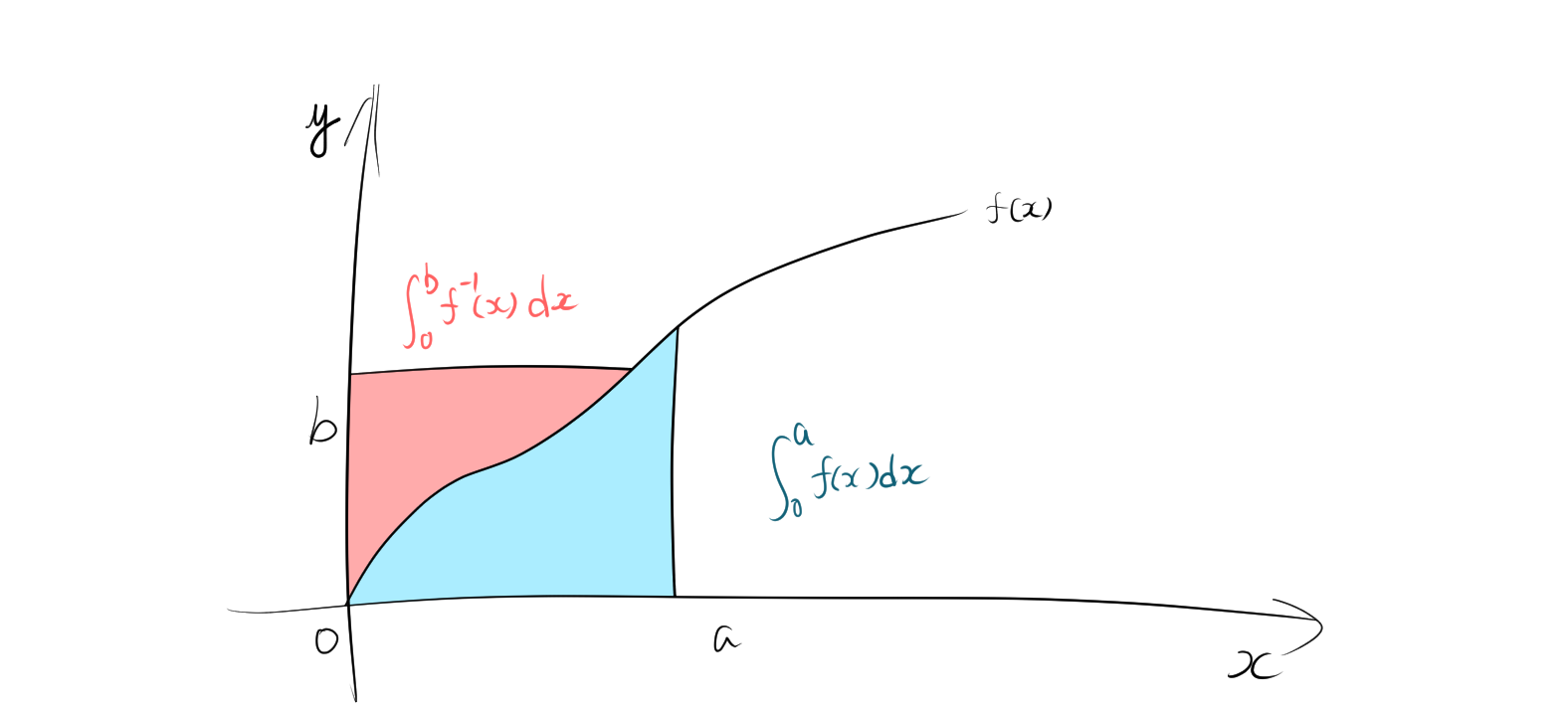
\[\int_0^a f(t) \, dt + \int_0^b g(t) \, dt \geq ab\]
ここで、
- \( f \) は \( f(0) = 0 \) を満たす単調増加関数。
- \( g \) は \( f \) の逆関数。
積分形の不等式は次の図が示すように明らかに成り立っていることがわかります。
3.1. 一般化
この、積分の不等式は先ほど紹介した不等式の一般化と呼ばれています。実際に\(f(x) = x^{p-1}\)、\(g(x) = x^{q-1}\) として積分を計算すると理由がわかります。
\[ \int_0^a t^{p-1} \, dt = \frac{a^p}{p}, \quad \int_0^b t^{q-1} \, dt = \frac{b^q}{q} \]
よって、先ほど紹介した不等式の形になる。
\[ \frac{a^p}{p} + \frac{b^q}{q} \geq ab \]